题目内容
设L是坐标平面第二、四象限内坐标轴的夹角平分线.(1)在L上求一点C,使它和两点A(-4,-2)、B(5,3
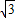 -2)的距离相等;
-2)的距离相等;(2)求∠BAC的度数;
(3)求(1)中△ABC的外接圆半径R及以AB为弦的弓形ABC的面积.
【答案】分析:(1)设C(x,-x),根据两点间的距离公式(勾股定理)得到方程,求出方程的解即可;
(2)作BE⊥AC于E,求出AC,根据勾股定理求出BC,得到AC=BC,求出CE、BE,求出∠A即可;
(3)求出△ABC的高CD的长,求出AB的长,根据圆周角定理求出∠AO'B,证△AO'B≌△ACB,推出R=AC,根据三角形的面积和扇形的面积公式求出即可.
解答: 解:(1)设C(x,-x),
解:(1)设C(x,-x),
∵AC=BC,
根据勾股定理得:(x+4)2+(-x+2)2=(x-5)2+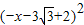 ,
,
解得:x=2,
∴C(2,-2).
答:点C的坐标是(2,-2).
(2)AC∥x轴,作BE⊥AC于E,
∴AC=2+4=6,
由勾股定理得:BC=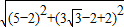 =6,
=6,
∴AC=BC=6,BE=3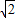 ,CE=3,
,CE=3,
∴∠ABC=∠BAC=30°.
答:∠BAC的度数是30°.
(3)设圆心为O’,
∵∠ACB=180°∠A-∠ABC=120°,
∴∠AO'B=360°-2×120°=120°,
∵AO=OB,
∴∠OAB=∠OBA=30°,
∴∠OAB=∠CAB,∠OBA=∠CBA,AB=AB,
∴△AO'B≌△ACB,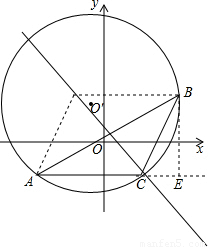
∴AO=OB=AC=BC=6,
∴R=6,
连接O'C交AB于D,
则CD⊥AB,
∵∠CAB=30°,
∴CD= AC=3,
AC=3,
由勾股定理得:AD=3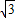 ,
,
∴AB=2AD=6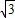 ,
,
∴S弓形ABC=S扇形OACB-S△ACB=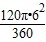 -
- ×6
×6 ×3=12π-9
×3=12π-9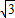 .
.
答:(1)中△ABC的外接圆半径R是6,以AB为弦的弓形ABC的面积是12π-9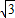 .
.
点评:本题主要考查对圆周角定理,三角形的面积,扇形的面积,勾股定理,两点间的距离公式,等腰三角形的性质,三角形的外接圆与外心,全等三角形的性质和判定等知识点的理解和掌握,综合运用这些性质进行推理和计算是解此题的关键.
(2)作BE⊥AC于E,求出AC,根据勾股定理求出BC,得到AC=BC,求出CE、BE,求出∠A即可;
(3)求出△ABC的高CD的长,求出AB的长,根据圆周角定理求出∠AO'B,证△AO'B≌△ACB,推出R=AC,根据三角形的面积和扇形的面积公式求出即可.
解答:
 解:(1)设C(x,-x),
解:(1)设C(x,-x),∵AC=BC,
根据勾股定理得:(x+4)2+(-x+2)2=(x-5)2+
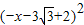 ,
,解得:x=2,
∴C(2,-2).
答:点C的坐标是(2,-2).
(2)AC∥x轴,作BE⊥AC于E,
∴AC=2+4=6,
由勾股定理得:BC=
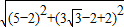 =6,
=6,∴AC=BC=6,BE=3
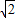 ,CE=3,
,CE=3,∴∠ABC=∠BAC=30°.
答:∠BAC的度数是30°.
(3)设圆心为O’,
∵∠ACB=180°∠A-∠ABC=120°,
∴∠AO'B=360°-2×120°=120°,
∵AO=OB,
∴∠OAB=∠OBA=30°,
∴∠OAB=∠CAB,∠OBA=∠CBA,AB=AB,
∴△AO'B≌△ACB,

∴AO=OB=AC=BC=6,
∴R=6,
连接O'C交AB于D,
则CD⊥AB,
∵∠CAB=30°,
∴CD=
 AC=3,
AC=3,由勾股定理得:AD=3
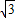 ,
,∴AB=2AD=6
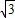 ,
,∴S弓形ABC=S扇形OACB-S△ACB=
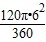 -
- ×6
×6 ×3=12π-9
×3=12π-9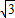 .
.答:(1)中△ABC的外接圆半径R是6,以AB为弦的弓形ABC的面积是12π-9
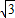 .
.点评:本题主要考查对圆周角定理,三角形的面积,扇形的面积,勾股定理,两点间的距离公式,等腰三角形的性质,三角形的外接圆与外心,全等三角形的性质和判定等知识点的理解和掌握,综合运用这些性质进行推理和计算是解此题的关键.

练习册系列答案
相关题目
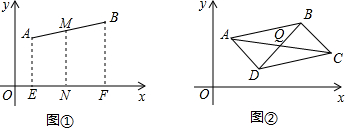 让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系.
让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系.

 -2)的距离相等;
-2)的距离相等;