Question

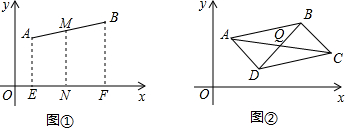让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系．
第一步：数轴上两点连线的中点表示的数．自己画一个数轴，如果点A、B分别表示-2、4，则线段AB的中点M表示的数是

1

． 再试几个，我们发现：数轴上连接两点的线段的中点所表示的数是这两点所表示数的平均数．
第二步；平面直角坐标系中两点连线的中点的坐标（如图①）为便于探索，我们在第一象限内取两点A（x₁，y₁），B（x₂，y₂），取线段AB的中点M，分别作A、B到x轴的垂线段AE、BF，取EF的中点N，则MN是梯形AEFB的中位线，故MN⊥x轴，利用第一步的结论及梯形中位线的性质，我们可以得到点M的坐标是（

x1+x2

2

，

y1+y2

2

 ）（用x₁，y₁，x₂，y₂表示），AEFB是矩形时也可以．我们的结论是：平面直角坐标系中连接两点的线段的中点的横（纵）坐标等于这两点的横（纵）坐标的平均数．
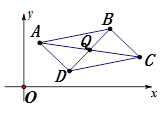
第三步：平面直角坐标系中平行四边形的顶点坐标之间的关系（如图②）在平面直角坐标系中画一个平行四边形ABCD，设A（x₁，y₁），B（x₂，y₂），C（x₃，y₃），D（x₄，y₄），则其对角线交点Q的坐标可以表示为Q（

x1+x3

2

，

y1+y3

2

），也可以表示为Q（

x2+x4

2

，

y2+y4

2

 ），经过比较，我们可以分别得出关于x₁，x₂，x₃，x₄及，y₁，y₂，y₃，y₄的两个等式是

x₁+x₃=x₂+x₄

和

y₁+y₃=y₂+y₄

． 我们的结论是：平面直角坐标系中平行四边形的对角顶点的横（纵）坐标的

和相等

．

Answer 1

分析：画出数轴即可求出第一步；先求出N是EF中点，求出N的横坐标，根据梯形的中位线性质求出纵坐标即可；根据平行四边形性质推出Q是AC和BD的中点，根据以上结论即可求出答案．

解答：解：第一步：故答案为：1，如图：．

解：∵MN是梯形AEFB的中位线，AE∥BF，
∴E、F的横坐标分别是x₁，x₂，
由第一步得出：N和M的横坐标是：

x1+x2

2

，MN=

AE+BF

2

=

y1+y2

2

，即是M的纵坐标，
故答案为：M(

x1+x2

2

，

y1+y2

2

)．

解：与第二步解法类似，根据平行四边形的性质得出QA=QC，QB=QD，推出：（

x1+x3

2

，

y1+y3

2

）或Q(

x2+x4

2

，

y2+y4

2

)，
故答案为：（

x1+x3

2

，

y1+y3

2

），（

x2+x4

2

，

y2+y4

2

）．
解：由第三步推出x₁+x₃=x₂+x₄    y₁+y₃=y₂+y₄，
故答案为：x₁+x₃=x₂+x₄    y₁+y₃=y₂+y₄，和相等．

点评：本题考查了平行四边形性质，梯形的中位线性质，点的坐标的应用，解此题的关键是得出规律，能通过作题培养学生分析问题和解决问题的能力，同时也培养了学生的理解能力和观察问题的能力，题型较好．