题目内容
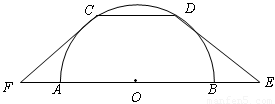
如图,CD是半圆O的一条弦,CD∥AB,延长OA、OB至F、E,使 ,联结FC、ED,CD=2,AB=6。
,联结FC、ED,CD=2,AB=6。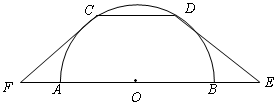
(1)求∠F的正切值;
(2)联结DF,与半径OC交于H,求△FHO的面积。
(1) ;(2)
;(2)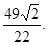
解析试题分析:(1)作ON⊥CD于点D,CM⊥AB于点M,先根据垂径定理及勾股定理求得CM的长,再根据正切函数的定义即可求得结果;
(2)由CD∥AB可得△CDH∽△OFH,再根据相似三角形的性质即可求得结果.
(1)作ON⊥CD于点D,CM⊥AB于点M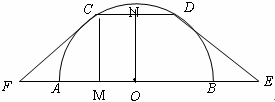
由题意得 ,
,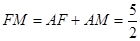
所以 ;
;
(2)如图所示:
∵CD∥AB
∴△CDH∽△OFH
∵
∴△FHO的面积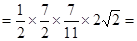
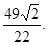
考点:垂径定理,勾股定理,锐角三角函数的定义,相似三角形的判定和性质
点评:本题知识点多,综合性强,是中考常见题,正确作出辅助线是解题的关键.

练习册系列答案
相关题目
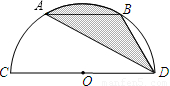
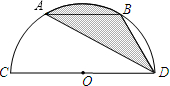 如图,CD是半圆O的直径,弦AB∥CD,且CD=6,∠ADB=30°,则阴影部分的面积是( )
如图,CD是半圆O的直径,弦AB∥CD,且CD=6,∠ADB=30°,则阴影部分的面积是( )| A、π | ||
B、
| ||
| C、3π | ||
| D、6π |
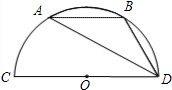 如图,CD是半圆O的直径,弦AB∥CD,且CD=6,∠ADB=30°,则∠AOB=
如图,CD是半圆O的直径,弦AB∥CD,且CD=6,∠ADB=30°,则∠AOB=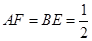 ,联结FC、ED,CD=2,AB=6。
,联结FC、ED,CD=2,AB=6。