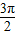题目内容
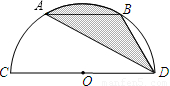
 如图,CD是半圆O的直径,弦AB∥CD,且CD=6,∠ADB=30°,则阴影部分的面积是( )
如图,CD是半圆O的直径,弦AB∥CD,且CD=6,∠ADB=30°,则阴影部分的面积是( )| A、π | ||
B、
| ||
| C、3π | ||
| D、6π |
分析:连接OA,OB,则阴影部分的面积=扇形AOB的面积,根据扇形的面积公式即可求解.
解答: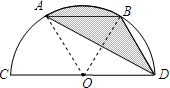 解:连接OA,OB.
解:连接OA,OB.
∵∠ADB=30°,
∴∠AOB=60°,
∵AB∥CD,
∴△ABD的面积=△AOB的面积,
∴阴影部分的面积=弓形AB的面积+△ABD的面积=弓形AB的面积+△AOB的面积
=扇形AOB的面积=
=
.
故选B.
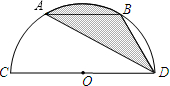
 解:连接OA,OB.
解:连接OA,OB.∵∠ADB=30°,
∴∠AOB=60°,
∵AB∥CD,
∴△ABD的面积=△AOB的面积,
∴阴影部分的面积=弓形AB的面积+△ABD的面积=弓形AB的面积+△AOB的面积
=扇形AOB的面积=
| 60π×32 |
| 360 |
| 3π |
| 2 |
故选B.
点评:本题主要考查了扇形的面积公式,正确理解阴影部分的面积=扇形AOB的面积是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
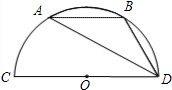 如图,CD是半圆O的直径,弦AB∥CD,且CD=6,∠ADB=30°,则∠AOB=
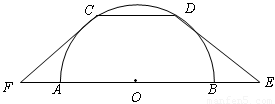
如图,CD是半圆O的直径,弦AB∥CD,且CD=6,∠ADB=30°,则∠AOB= ,联结FC、ED,CD=2,AB=6。
,联结FC、ED,CD=2,AB=6。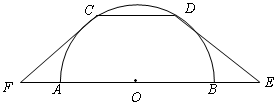
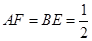 ,联结FC、ED,CD=2,AB=6。
,联结FC、ED,CD=2,AB=6。