题目内容
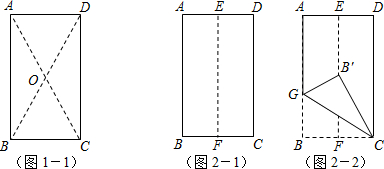
在图形的全等变换中,有旋转变换,翻折(轴对称)变换和平移变换.一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.(1)第一小组的同学发现,在如图1-1的矩形ABCD中,AC、BD相交于点O,Rt△ADC可以由Rt△ABC经过一种变换得到,请你写出这种变换的过程______.

(2)第二小组同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图2-1);再沿GC折叠,使点B落在EF上的点B′处(如图2-2),这样能得到∠B′GC的大小,你知道∠B′GC的大小是多少吗?请写出求解过程.
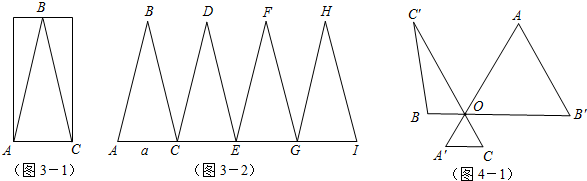
(3)第三小组的同学,在一个矩形纸片上按照图3-1的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图3-2.已知AH=AI,AC长为a,现以AD、AF和AH为三边构成一个新三角形,已知这个新三角形面积小于15
 ,请你帮助该小组求出a可能的最大整数值.
,请你帮助该小组求出a可能的最大整数值.
(4)探究活动结束后,老师给大家留下了一道探究题:
如图4-1,已知AA′=BB′=CC′=2,∠AOB′=∠BOC′=∠COA′=60°,请利用图形变换探究S△AOB′+S△BOC′+S△COA′与
 的大小关系.
的大小关系.
【答案】分析:(1)根据矩形是中心对称图形,可以将Rt△ABC旋转180°得到Rt△ADC而得出结论;
(2)连接BB',由题意得EF垂直平分BC,就有BB'=B'C,由翻折可得B'C=BC,从而△BB'C为等边三角形.就可以求出∠B'CB=60°;
(3)分别取CE、EG、GI的中点P、Q、R,连接DP、FQ、HR、AD、AF、AH,由BA=BC,根据平移变换的性质,就有△CDE、△EFG和△GHI都是等腰三角形,就有DP⊥CE,FQ⊥EG,HR⊥GI,由勾股定理就可以求出HR2=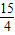 a2,从而得出新三角形三边的值,从而得出结论;
a2,从而得出新三角形三边的值,从而得出结论;
(4)将△BOC'沿BB'方向平移2个单位,所移成的三角形记为△B'PR,将△COA'沿A'A方向平移2个单位,所移成的三角形记为△AQR.由条件可以得出△AQR为等边三角形,由等边三角形的性质就可以求出△AQR的面积为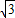 ,从而就可以得出结论.
,从而就可以得出结论.
解答:解:(1)将△ABC绕点O旋转180°后可得到△ADC;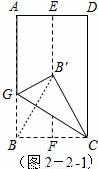
故答案为:将△ABC绕点O旋转180°后可得到△ADC.
(2)如图2-2-1,连接BB',由题意得EF垂直平分BC,
∴BB'=B'C,由翻折可得,
∴B'C=BC,
∴△BB'C为等边三角形.
∴∠B'CB=60°,
∴∠B'CG=30°,
∵∠GB′C=90°,
∴∠B'GC=60°;
(3)如图3-1-1,分别取CE、EG、GI的中点P、Q、R,连接DP、FQ、HR、AD、AF、AH,
∵BA=BC,根据平移变换的性质,
∴△CDE、△EFG和△GHI都是等腰三角形,
∴DP⊥CE,FQ⊥EG,HR⊥GI,GR=EQ=CP=0.5a,DP=FQ=HR.
∵AC=a,
∴AI=4a.
∵AH=AI,
∴AH=4a,AR=3.5a.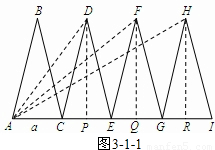
∴AH2=16a2.
在Rt△AHR中,AH2=HR2+AR2,
16a2=HR2+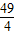 a2,
a2,
HR2=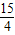 a2,
a2,
∴DP2=FQ2=HR2=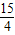 a2,
a2,
在Rt△ADP和Rt△AFQ中,由勾股定理,得
AD2=AP2+DP2=6a2,AF2=AQ2+FQ2=10a2,
∴AH2=AD2+AF2,
∴新三角形为直角三角形,
∴新三角形三边长为4a、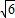 a、
a、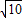 a.
a.
其面积为:
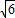 a×
a×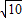 a=
a=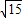 a2.
a2.
∵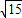 a2<15
a2<15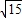 ,
,
∴a2<15
∴a的最大整数值为3.
(4)如图4-1-1,将△BOC'沿BB'方向平移2个单位,所移成的三角形记为△B'PR,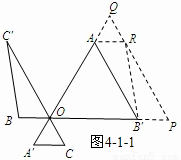
将△COA'沿A'A方向平移2个单位,所移成的三角形记为△AQS.连接PQ,
∵QR+PR=OC+OC',
∴Q、R、P三点共线.
∵OQ=OA+AQ=OA+OA'=AA'=2,OP=OB'+B'P=OB'+OB=BB'=2.且∠QOP=60°,
∴△OPQ为等边三角形.
∴PQ=OQ=OP=2.
∵RP=OC′,QS=OC,
∴RP+QS=OC′+OC=CC′=2=PQ,
∴R、S重合.
∴S△QOP=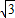 ,
,
∵S△AOB+S△BOC+S△COA=S△AOB+S△B'PR+S△PQA<S△OPQ,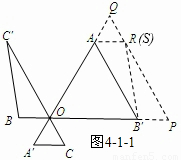
∴S△AOB+S△BOC+S△COA<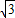 .
.
点评:本题考查了旋转变换的运用,翻折变换的运用,平移变换的运用,等边三角形的性质的运用,勾股定理的运用,等腰三角形的性质的运用,三角形的面积公式的运用.本题的综合性较强要求学生熟练的运用图形变换解题是关键.
(2)连接BB',由题意得EF垂直平分BC,就有BB'=B'C,由翻折可得B'C=BC,从而△BB'C为等边三角形.就可以求出∠B'CB=60°;
(3)分别取CE、EG、GI的中点P、Q、R,连接DP、FQ、HR、AD、AF、AH,由BA=BC,根据平移变换的性质,就有△CDE、△EFG和△GHI都是等腰三角形,就有DP⊥CE,FQ⊥EG,HR⊥GI,由勾股定理就可以求出HR2=
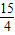 a2,从而得出新三角形三边的值,从而得出结论;
a2,从而得出新三角形三边的值,从而得出结论;(4)将△BOC'沿BB'方向平移2个单位,所移成的三角形记为△B'PR,将△COA'沿A'A方向平移2个单位,所移成的三角形记为△AQR.由条件可以得出△AQR为等边三角形,由等边三角形的性质就可以求出△AQR的面积为
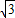 ,从而就可以得出结论.
,从而就可以得出结论.解答:解:(1)将△ABC绕点O旋转180°后可得到△ADC;

故答案为:将△ABC绕点O旋转180°后可得到△ADC.
(2)如图2-2-1,连接BB',由题意得EF垂直平分BC,
∴BB'=B'C,由翻折可得,
∴B'C=BC,
∴△BB'C为等边三角形.
∴∠B'CB=60°,
∴∠B'CG=30°,
∵∠GB′C=90°,
∴∠B'GC=60°;
(3)如图3-1-1,分别取CE、EG、GI的中点P、Q、R,连接DP、FQ、HR、AD、AF、AH,
∵BA=BC,根据平移变换的性质,
∴△CDE、△EFG和△GHI都是等腰三角形,
∴DP⊥CE,FQ⊥EG,HR⊥GI,GR=EQ=CP=0.5a,DP=FQ=HR.
∵AC=a,
∴AI=4a.
∵AH=AI,
∴AH=4a,AR=3.5a.

∴AH2=16a2.
在Rt△AHR中,AH2=HR2+AR2,
16a2=HR2+
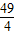 a2,
a2,HR2=
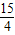 a2,
a2,∴DP2=FQ2=HR2=
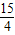 a2,
a2,在Rt△ADP和Rt△AFQ中,由勾股定理,得
AD2=AP2+DP2=6a2,AF2=AQ2+FQ2=10a2,
∴AH2=AD2+AF2,
∴新三角形为直角三角形,
∴新三角形三边长为4a、
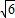 a、
a、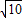 a.
a.其面积为:

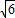 a×
a×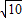 a=
a=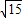 a2.
a2.∵
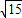 a2<15
a2<15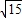 ,
,∴a2<15
∴a的最大整数值为3.
(4)如图4-1-1,将△BOC'沿BB'方向平移2个单位,所移成的三角形记为△B'PR,

将△COA'沿A'A方向平移2个单位,所移成的三角形记为△AQS.连接PQ,
∵QR+PR=OC+OC',
∴Q、R、P三点共线.
∵OQ=OA+AQ=OA+OA'=AA'=2,OP=OB'+B'P=OB'+OB=BB'=2.且∠QOP=60°,
∴△OPQ为等边三角形.
∴PQ=OQ=OP=2.
∵RP=OC′,QS=OC,
∴RP+QS=OC′+OC=CC′=2=PQ,
∴R、S重合.
∴S△QOP=
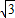 ,
,∵S△AOB+S△BOC+S△COA=S△AOB+S△B'PR+S△PQA<S△OPQ,

∴S△AOB+S△BOC+S△COA<
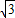 .
.点评:本题考查了旋转变换的运用,翻折变换的运用,平移变换的运用,等边三角形的性质的运用,勾股定理的运用,等腰三角形的性质的运用,三角形的面积公式的运用.本题的综合性较强要求学生熟练的运用图形变换解题是关键.

练习册系列答案
相关题目




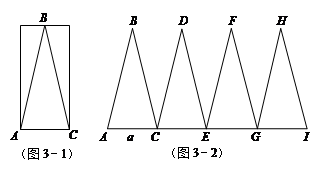

 的大小关系.
的大小关系.


 的大小关系.
的大小关系.


 的大小关系.
的大小关系.