题目内容
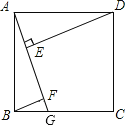
【题目】如图,四边形ABCD是正方形,点G是BC上的任意一点,DE⊥AG于E,BF∥DE,交AG于F.那AF与BF+EF相等吗?请说明理由.
【答案】相等,理由见详解.
【解析】
由四边形ABCD为正方形,可得出∠BAD为90°,AB=AD,进而得到∠BAG与∠EAD互余,又DE垂直于AG,得到∠EAD与∠ADE互余,根据同角的余角相等可得出∠ADE=∠BAF,利用AAS可得出三角形ABF与三角形ADE全等,利用全等三角的对应边相等可得出BF=AE,由AE+EF=AF,等量代换可得证.
解:相等
如图,∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠BAG+∠EAD=90°,
∵DE⊥AG,
∴∠AED=90°,
∴∠EAD+∠ADE=90°,
∴∠ADE=∠BAF,
又∵BF∥DE,
∴BF⊥AG
∴∠AFB=∠AED=90°,
在△AED和△BFA中,
∵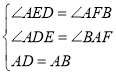 ,
,
∴△AED≌△BFA(AAS),
∴BF=AE,
∵AE+EF=AF,
∴BF+EF= AF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某大型超市上周日购进新鲜黄瓜1000公斤,进价为每公斤1.5元,受暴发的“毒黄瓜”的影响,销售价格出现较大的波动,表中为一周内黄瓜销告价格的涨跌情况(涨为正,跌为负,其中星期一的销售价格是与进价比较,单位:元):
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每公斤销售价涨跌 (与前一天比较) | +0.3 | +0.4 | -0.5 | -0.6 | -0.7 | +0.1 |
(1)到星期二时,每公斤黄瓜的售价是多少元?
(2)本周最低售价是每公斤多少元?
(3)已知截止到星期五,已卖出黄瓜700公斤,销售总额为935元.如果超市星期六能将剩下的黄瓜全部卖出,不考虑损耗等其他因素,请算算该超市本周销售黄瓜是盈还是亏,盈亏是多少.