题目内容
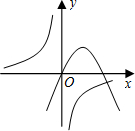反比例函数与二次函数在同一平面直角坐标系中的大致图象如图所示，则它们的解析式可能分别是（ ）A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
分析：本题可先由反比例函数的图象得到字母系数的正负，再与二次函数的图象相比较看是否一致．
解答：解：双曲线的两支分别位于二、四象限，即k＜0；
A、当k＜0时，物线开口方向向下，对称轴x=-
=
＜0，不符合题意，错误；
B、当k＜0时，物线开口方向向下，对称轴x=-
=-
＞0，符合题意，正确；
C、当-k＜0时，即k＞0，物线开口方向向上，不符合题意，错误；
D、当-k＜0时，物线开口方向向下，但对称轴x=-
=-
＜0，不符合题意，错误．
故选B．
A、当k＜0时，物线开口方向向下，对称轴x=-
| b |
| 2a |
| 1 |
| 2k |
B、当k＜0时，物线开口方向向下，对称轴x=-
| b |
| 2a |
| 1 |
| 2k |
C、当-k＜0时，即k＞0，物线开口方向向上，不符合题意，错误；
D、当-k＜0时，物线开口方向向下，但对称轴x=-
| b |
| 2a |
| 1 |
| 2k |
故选B．
点评：解决此类问题步骤一般为：（1）根据图象的特点判断a取值是否矛盾；（2）根据二次函数图象判断其对称轴是否符合要求．
练习册系列答案
相关题目
（2012•重庆模拟）草莓是对蔷薇科草莓属植物的通称，属多年生草本植物，草莓的外观呈心形，鲜美红嫩，果肉多汁，含有特殊的浓郁水果芳香，草莓营养价值高，含丰富维生素C，有帮助消化的功效，与此同时，草莓还可以巩固齿龈，清新口气，润泽喉部．我市某草莓种植基地去年第x个月种植草莓的亩数y（亩），与x（1≤x≤12，且x为整数）之间的函数关系如表：