题目内容
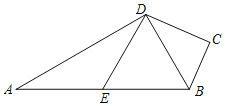
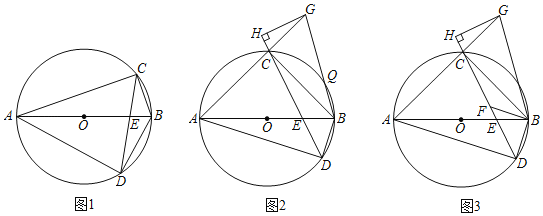
【题目】如图,四边形ADBC内接于⊙O,AB为⊙O的直径,对角线AB、CD相交于点E.
(1)求证:∠BCD+∠ABD=90°;
(2)点G在AC的延长线上,连接BG,交⊙O于点Q,CA=CB,∠ABD=∠ABG,作GH⊥CD,交DC的延长线于点H,求证:GQ=![]() GH.
GH.
(3)在(2)的条件下,过点B作BF∥AD,交CD于点F,GH=3CH,若CF=4![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)⊙O的半径为2![]() .
.
【解析】
(1)由圆周角定理可得∠ACB=90°=∠ADB,即可得结论;
(2)过点A作AM⊥AD,交DC的延长线于点M,连接AQ,MG,通过证明△AMG≌△AQG,可得MG=GQ,∠AMG=∠AQG=90°,可证HM=HG,即可得结论;
(3)延长MG与DB的交点为N,延长BF交AG于点P,通过证明△PCF∽△GCM,可得MC=CF=![]() ,MG=PF,通过证明△HGC∽△DAB,可得AD=3BD,由MD=
,MG=PF,通过证明△HGC∽△DAB,可得AD=3BD,由MD=![]() AD,可求BD的长,即可求⊙O的半径.
AD,可求BD的长,即可求⊙O的半径.
证明:(1)∵AB是直径,
∴∠ACB=90°=∠ADB,
∴∠ACD+∠BCD=90°,
∵∠ACD=∠ABD,
∴∠BCD+∠ABD=90°;
(2)如图,过点A作AM⊥AD,交DC的延长线于点M,连接AQ,MG.

∵AB是直径
∴∠AQB=∠ACB=∠ADB=90°
∵CA=CB
∴∠ABC=∠BAC=45°
∴∠ADC=∠ABC=45°
∵AM⊥AD
∴∠ADM=∠AMD=45°
∴AM=AD,
∵∠ABD=∠ABG,∠AQB=∠ADB,AB=AB
∴△AQB≌△ADB(AAS)
∴AD=AQ,∠BAD=∠BAQ
∴AQ=AM,
∵∠CAB=45°
∴∠BAD+∠MAG=45°,∠BAQ+∠GAQ=45°
∴∠MAG=∠GAQ,且AM=AD,AG=AG
∴△AMG≌△AQG(SAS)
∴MG=GQ,∠AMG=∠AQG=90°
∵∠AMD=45°
∴∠GMH=45°
∵GH⊥MD
∴∠HMG=∠HGN=45°
∴HM=HG
∴MG=![]() HG
HG
∴GQ=![]() HG;
HG;
(3)如图,延长MG与DB的交点为N,延长BF交AG于点P.

∵∠MAD=∠AMN=∠ADB=90°
∴四边形ADNM是矩形,且AD=AM
∴四边形ADNM是正方形
∴AM=AD=MN=DN,MN∥AD
∴∠GAD=∠AGM=∠AGB
∵BF∥AD
∴∠GPB=∠GAD=∠AGB
∴BG=BP,且BC⊥AG
∴PC=CG
∵BP∥AD∥MN
∴△PCF∽△GCM
∴![]() =1
=1
∴MC=CF=![]() ,MG=PF,
,MG=PF,
∵∠ACD=∠HCG=∠ABD,∠GHC=∠ADB=90°
∴△HGC∽△DAB
∴![]() ,且GH=3CH,
,且GH=3CH,
∴AD=3BD
∵∠CDB=∠CAB=45°,∠FBD=90°
∴FD=![]() BD
BD
∵AD=AM,∠MAD=90°
∴MD=![]() AD
AD
∴![]() +
+![]() +
+![]() BD=
BD=![]() ×3BD
×3BD
∴BD=4
∴AD=12
∴AB=![]() =
=![]()
∴⊙O的半径为![]() .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案