题目内容
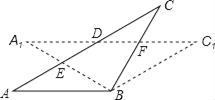
【题目】已知:![]() 内接于
内接于![]() ,过点
,过点![]() 作直线
作直线![]() ,
,![]() 为非直径的弦,且
为非直径的弦,且![]() 是
是![]() 的切线
的切线
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,
,![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求由弧
,求由弧![]() 、线段
、线段![]() 和
和![]() 所围成的图形的面积.
所围成的图形的面积.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连结![]() 并延长交
并延长交![]() 于
于![]() ,连结
,连结![]() ,由圆周角定理可知∠H=∠A,∠HCB=90°,根据切线性质可知∠OBF=90°,根据
,由圆周角定理可知∠H=∠A,∠HCB=90°,根据切线性质可知∠OBF=90°,根据![]() ,
,![]() ,可证明
,可证明![]() H=∠CBF,即可证明∠A=∠CBF;(2)在Rt△HCB中,由BC=2,∠H=∠A=30°得到HB=4,OB=2,又∠BOM=2∠A=60°,根据三角函数可以求出MB,而
H=∠CBF,即可证明∠A=∠CBF;(2)在Rt△HCB中,由BC=2,∠H=∠A=30°得到HB=4,OB=2,又∠BOM=2∠A=60°,根据三角函数可以求出MB,而
S=S△OBM-S扇形OBC=,由此即可求出由弧BC、线段BM和CM所围成的图形的面积.
![]() 连结
连结![]() 并延长交
并延长交![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() .
.
∵![]() 是直径,
是直径,
∴![]() ,
,
∴![]() .
.
又∵![]() 是半径,
是半径,![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
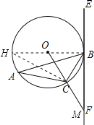
∴![]() ;
;
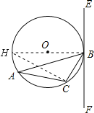
![]() ∵在
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
![]() ,
,
故由弧![]() 、线段
、线段![]() 和
和![]() 所围成的图形的面积为
所围成的图形的面积为![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目