题目内容
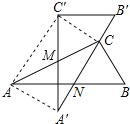
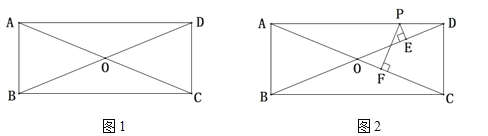
【题目】如图，在四边形ABCD中，AC、BD相交于点O，AD∥BC，∠ADC=∠ABC，OA=OB．
（1）如图1，求证：四边形ABCD为矩形；
（2）如图2，P是AD边上任意一点，PE⊥BD，PF⊥AC，E、F分别是垂足，若AD=12，AB=5，求PE+PF的值．
【答案】（1）证明见解析 （2）
【解析】
（1）通过平行线的性质可得
，再根据
可得
，即可证明
，即可证明四边形ABCD是平行四边形，再根据
，即可证明四边形ABCD是矩形；
（2）连接OP，根据矩形的性质和勾股定理得
，再根据矩形和三角形的面积公式即可求解．
（1）∵
∴
∵
∴
∴
∴
∴四边形ABCD是平行四边形
∵
∴四边形ABCD是矩形；
（2）连接OP，
∵四边形ABCD是矩形
∴
在△BAD中，
由勾股定理得
∴
∵矩形的面积是
∴△AOD的面积是
∵△APO、△POD是同底的三角形
∴
∴
∴
故PE+PF的值．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
