题目内容
【题目】探究证明:
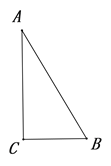
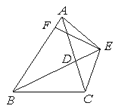
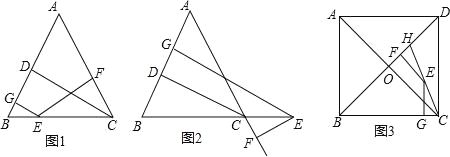
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
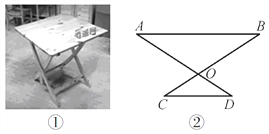
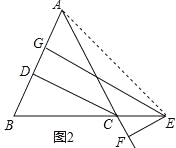
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
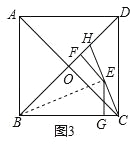
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .
【答案】(1)证明见解析
(2)CD=EG﹣EF,
(3)5![]() .
.

【解析】
试题分析:(1)根据S△ABC=S△ABE+S△ACE,得到![]() ABCD=
ABCD=![]() ABEG+
ABEG+![]() ACEF,根据等式的性质即可得到结论;
ACEF,根据等式的性质即可得到结论;
(2)由于S△ABC=S△ABE﹣S△ACE,于是得到![]() ABCD=
ABCD=![]() ABEG﹣
ABEG﹣![]() ACEF,根据等式的性质即可得到结论;
ACEF,根据等式的性质即可得到结论;
(3)根据正方形的性质得到AB=BC=10,∠ABC=90°,AC⊥BD,根据勾股定理得到AC=10![]() ,由于S△BCH=S△BCE+S△BHE,得到
,由于S△BCH=S△BCE+S△BHE,得到![]() BHOC=
BHOC=![]() BCEG+
BCEG+![]() BHEF,根据等式的性质即可得到结论.
BHEF,根据等式的性质即可得到结论.
试题解析:(1)如图1,连接AE,
∵EG⊥AB,EF⊥AC,CD⊥AB,
∵S△ABC=S△ABE+S△ACE,
∴![]() ABCD=
ABCD=![]() ABEG+
ABEG+![]() ACEF,
ACEF,
∵AB=AC,
∴CD=EG+EF;
(2)CD=EG﹣EF,
理由:连接AE,
∵EG⊥AB,EF⊥AC,CD⊥AB,
∵S△ABC=S△ABE﹣S△ACE,
∴![]() ABCD=
ABCD=![]() ABEG﹣
ABEG﹣![]() ACEF,
ACEF,
∵AB=AC,
∴CD=EG﹣EF;
故答案为:CD=EG﹣EF;
(3)∵四边形ABCD是正方形,
∴AB=BC=10,∠ABC=90°,AC⊥BD,
∴AC=10![]() ,
,
∴OC=![]() AC=5
AC=5![]() ,
,
连接BE.
∵EF⊥BD于点F,EG⊥BC于点G,
∵S△BCH=S△BCE+S△BHE,
∴![]() BHOC=
BHOC=![]() BCEG+
BCEG+![]() BHEF,
BHEF,
∴OC=EG+EF=5![]() ,
,
故答案为:5![]() .
.




【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.