题目内容
如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC,延长EC到点P,连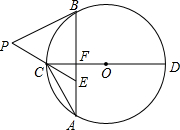 接PB.使PB=PE.
接PB.使PB=PE.
(1)在以下5个结论中:一定成立的是
①
=
;②OF=CF;③BF=AF;④AC2=AE•AB;⑤PB是⊙O的切线.
(2)若⊙O的半径为8cm.AE:EF=2:1.求弓形ACB的面积.
 接PB.使PB=PE.
接PB.使PB=PE.(1)在以下5个结论中:一定成立的是
①③④⑤
①③④⑤
(只需将结论的代号填人题中的横线上)①
 |
| AC |
 |
| BC |
(2)若⊙O的半径为8cm.AE:EF=2:1.求弓形ACB的面积.
分析:(1)连接BC,OB,OA,根据垂径定理即可判断①②③;证△ACE和△ACB相似推出比例式,即可判断④;证出OB⊥PB,根据切线的判定定理判断⑤即可;
(2)弓形ACB的面积等于扇形OAB的面积减去△AOB的面积,设AE=2a,EF=a,则CE=2a,在Rt△OBF中,根据勾股定理求出a,根据含30度角的直角三角形求出圆心角AOB的度数,根据扇形的面积和三角形的面积求出即可.
(2)弓形ACB的面积等于扇形OAB的面积减去△AOB的面积,设AE=2a,EF=a,则CE=2a,在Rt△OBF中,根据勾股定理求出a,根据含30度角的直角三角形求出圆心角AOB的度数,根据扇形的面积和三角形的面积求出即可.
解答: 解:(1)连接BC,OB,OA,
解:(1)连接BC,OB,OA,
∵AB⊥CD,CD是圆的直径,
∴BC=AC,弧AC=弧BC,BF=AF,∴①③正确;
∴∠CAB=∠CBA,
∵CE=AE,
∴∠CAB=∠ACE=∠CBA,
∵∠CAB=∠CAB,
∴△CAE∽△BAC,
∴
=
,
∴AC2=AE•AB,∴④正确;
∵PB=PE,
∴∠PBA=∠PEB,
∵∠PEB=∠CAB+∠ECA=2∠CAB=2∠CBF,
∴∠PBC=∠CBE,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC+∠CBP=∠OCB+∠CBA=90°,
即OB⊥PB,
∵OB是圆O的半径,
∴PB是圆O的切线,∴⑤正确;
根据已知条件不能推出CF=OF,∴②错误;
故答案为:①③④⑤.
(2)设AE=2a,EF=a,则CE=2a,由勾股定理得:CF=
a,
BF=AF=3a,
在Rt△OBF中,由勾股定理得:OB2=BF2+OF2,
∴82=(3a)2+(8-
a)2,
∴a=
,
∴OF=8-
×
=4,
∵OB=8,
∴∠FBO=30°,
∴∠BOA=2×60°=120°,
∴弓形ACB的面积等于扇形OAB的面积减去△AOB的面积,
即:
-
×6×
×4=(
π-16
)(cm2),
答:弓形ACB的面积是
π-16
cm2
 解:(1)连接BC,OB,OA,
解:(1)连接BC,OB,OA,∵AB⊥CD,CD是圆的直径,
∴BC=AC,弧AC=弧BC,BF=AF,∴①③正确;
∴∠CAB=∠CBA,
∵CE=AE,
∴∠CAB=∠ACE=∠CBA,
∵∠CAB=∠CAB,
∴△CAE∽△BAC,
∴
| AC |
| AE |
| AB |
| AC |
∴AC2=AE•AB,∴④正确;
∵PB=PE,
∴∠PBA=∠PEB,
∵∠PEB=∠CAB+∠ECA=2∠CAB=2∠CBF,
∴∠PBC=∠CBE,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC+∠CBP=∠OCB+∠CBA=90°,
即OB⊥PB,
∵OB是圆O的半径,
∴PB是圆O的切线,∴⑤正确;
根据已知条件不能推出CF=OF,∴②错误;
故答案为:①③④⑤.
(2)设AE=2a,EF=a,则CE=2a,由勾股定理得:CF=
| 3 |
BF=AF=3a,
在Rt△OBF中,由勾股定理得:OB2=BF2+OF2,
∴82=(3a)2+(8-
| 3 |
∴a=
4
| ||
| 3 |
∴OF=8-
4
| ||
| 3 |
| 3 |
∵OB=8,
∴∠FBO=30°,
∴∠BOA=2×60°=120°,
∴弓形ACB的面积等于扇形OAB的面积减去△AOB的面积,
即:
| 120π×82 |
| 360 |
| 1 |
| 2 |
4
| ||
| 3 |
| 64 |
| 3 |
| 3 |
答:弓形ACB的面积是
| 64 |
| 3 |
| 3 |
点评:本题综合考查了等腰三角形的性质,勾股定理,相似三角形的性质和判定,垂径定理,含30度角的直角三角形性质,三角形的面积,扇形的面积,切线的判定等知识点,此题综合性比较强,有一定的难度,对学生有较高的要求,但题型较好.

练习册系列答案
相关题目
 如图,已知⊙O的弦AB、CD相交于点E,
如图,已知⊙O的弦AB、CD相交于点E, |
| AC |
 |
| BD |
| A、60° | B、100° |
| C、80° | D、130° |
 如图,已知⊙O的弦AB、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=2
如图,已知⊙O的弦AB、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=2| 5 |
| A、4cm | ||
| B、3cm | ||
| C、5cm | ||
D、
|
 如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=EB.
如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=EB. 23、如图,已知⊙O的弦AB垂直于直径CD,垂足为F,连接CA、CB.
23、如图,已知⊙O的弦AB垂直于直径CD,垂足为F,连接CA、CB. 如图,已知⊙O的弦AC=2cm,∠ABC=45°,则图中阴影部分的面积是
如图,已知⊙O的弦AC=2cm,∠ABC=45°,则图中阴影部分的面积是