题目内容
 如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=EB.
如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC=EB.(1)求证:△CEB∽△CBD;
(2)若CE=3,CB=5,求DE的长.
分析:(1)根据有两组角对应相等的两个三角形相似来判定其相似;
(2)根据相似三角形的对应边成比例先求出CD的长,已知CE的长,那么DE的长就容易求得了.
(2)根据相似三角形的对应边成比例先求出CD的长,已知CE的长,那么DE的长就容易求得了.
解答:(1)证明:∵弦CD垂直于直径AB,
∴BC=BD.
∴∠C=∠D.
又∵EC=EB,
∴∠C=∠CBE.
∴∠D=∠CBE.
又∵∠C=∠C,
∴△CEB∽△CBD.
(2)解:∵△CEB∽△CBD,
∴
=
.
∴CD=
=
=
.
∴DE=CD-CE=
-3=
.
∴BC=BD.
∴∠C=∠D.
又∵EC=EB,
∴∠C=∠CBE.
∴∠D=∠CBE.
又∵∠C=∠C,
∴△CEB∽△CBD.
(2)解:∵△CEB∽△CBD,
∴
| CE |
| CB |
| CB |
| CD |
∴CD=
| CB2 |
| CE |
| 52 |
| 3 |
| 25 |
| 3 |
∴DE=CD-CE=
| 25 |
| 3 |
| 16 |
| 3 |
点评:考查了相似三角形的判定和性质,难易程度适中.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,已知⊙O的弦AB、CD相交于点E,
如图,已知⊙O的弦AB、CD相交于点E, |
| AC |
 |
| BD |
| A、60° | B、100° |
| C、80° | D、130° |
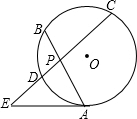 如图,已知⊙O的弦AB、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=2
如图,已知⊙O的弦AB、CD相交于点P,PA=4cm,PB=3cm,PC=6cm,EA切⊙O于点A,AE与CD的延长线交于点E,若AE=2| 5 |
| A、4cm | ||
| B、3cm | ||
| C、5cm | ||
D、
|
 23、如图,已知⊙O的弦AB垂直于直径CD,垂足为F,连接CA、CB.
23、如图,已知⊙O的弦AB垂直于直径CD,垂足为F,连接CA、CB. 如图,已知⊙O的弦AC=2cm,∠ABC=45°,则图中阴影部分的面积是
如图,已知⊙O的弦AC=2cm,∠ABC=45°,则图中阴影部分的面积是