题目内容
如图是一块直角三角形木板，∠C=90°，AB=5cm，AC=4cm，现要把它加工成一个正方形，请你设计一个方案，怎样裁才能使正方形的面积最大？并求出这个最大正方形的边长．
分析：首先根据勾股定理求得BC的长，然后分别求得正方形的其中两条边在直角三角形的两条直角边上的正方形的面积和以正方形的一边在直角三角形的斜边上的正方形的面积，再进一步比较它们的大小即可．
解答：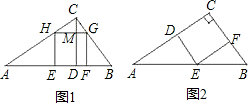
解：BC=
=
=3．
设正方形的边长为xcm，
方案①，如图1，正方形EFGH为设计正方形，
因为HG∥AB，
所以
=
，
又CD=
，CM=
-x，
则
=
，
解x=
；
方案②，如图2，正方形CDEF为设计正方形，
因为DE∥BC，
所以
=
，
即
=
，
解得x=
，
因为
＜
，
所以根据方案②的设计可得面积最大正方形，这时边长为
．
解：BC=| AB2-AC2 |
| 52-42 |
设正方形的边长为xcm，
方案①，如图1，正方形EFGH为设计正方形，
因为HG∥AB，
所以
| HG |
| AB |
| CM |
| CD |
又CD=
| 12 |
| 5 |
| 12 |
| 5 |
则
| x |
| 5 |
| ||
|
解x=
| 60 |
| 37 |
方案②，如图2，正方形CDEF为设计正方形，
因为DE∥BC，
所以
| DE |
| BC |
| AD |
| AC |
即
| x |
| 3 |
| 4-x |
| 4 |
解得x=
| 12 |
| 7 |
因为
| 60 |
| 37 |
| 12 |
| 7 |
所以根据方案②的设计可得面积最大正方形，这时边长为
| 12 |
| 7 |
点评：此题综合运用了勾股定理以及相似三角形的判定及性质．
练习册系列答案
阅读快车系列答案
相关题目
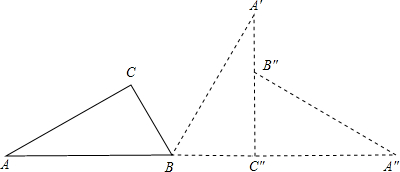
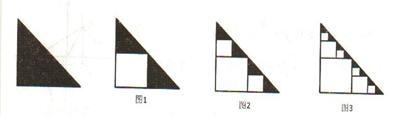
；再分别从剩下的两个三角形内用同样的方式裁剪下两个正方形,如图2所示,设所得到的剩余部分的面积为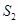
；再分别从剩余的四个三角形内用同样的方式裁剪下四个正方形,如图3所示,设所得到的剩余部分的面积为
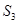；.........,如此下去,第n个裁剪后得到的剩余部分面积
=
．
如图是一块直角三角形木板，∠C=90°，AB=5cm，AC=4cm，现要把它加工成一个正方形，请你设计一个方案，怎样裁才能使正方形的面积最大？并求出这个最大正方形的边长．