��Ŀ����
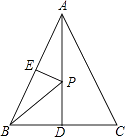
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����COD����CD�ĶԳ�ͼ��Ϊ��CED��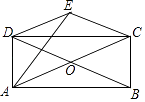
��1����֤���ı���OCED�����Σ�
��2������AE����AB=6cm��BC= ![]() cm��
cm��
����sin��EAD��ֵ��
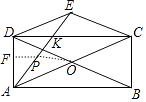
������PΪ�߶�AE��һ���㣨�����A�غϣ�������OP��һ����Q�ӵ�O��������1cm/s���ٶ����߶�OP�����˶�����P������1.5cm/s���ٶ����߶�PA�����˶�����A�������A��ֹͣ�˶�������Q������·���˶�����A����Ҫ��ʱ�����ʱ����AP�ij��͵�Q����ȫ�������ʱ�䣮
���𰸡�
��1��
֤�������ı���ABCD�Ǿ��Σ�
��OD=OB=OC=OA��
�ߡ�EDC�͡�ODC����CD�Գƣ�
��DE=DO��CE=CO��
��DE=EC=CO=OD��
���ı���CODE�����Σ�
��2��
�⣺����AE��CD��K��
���ı���CODE�����Σ�
��DE��AC��DE=OC=OA��
�� ![]() =
= ![]() =
= ![]()
��AB=CD=6��
��DK=2��CK=4��
��Rt��ADK��AK= ![]() =
= ![]() =3��
=3��
��sin��DAE= ![]() =
= ![]() ��
��
����PF��AD��F����֪PF=APsin��DAE= ![]() AP��
AP��
�ߵ�Q���˶�ʱ��t= ![]() +
+ ![]() =OP+
=OP+ ![]() AP=OP+PF��
AP=OP+PF��
�൱O��P��F����ʱ��OP+PF��ֵ��С����ʱOF�ǡ�ACD����λ�ߣ�
��OF= ![]() CD=3��AF=
CD=3��AF= ![]() AD=
AD= ![]() ��PF=
��PF= ![]() DK=1��
DK=1��
��AP= ![]() =
= ![]() ��
��
�൱��Q������·���˶�����A����Ҫ��ʱ�����ʱ��AP�ij�Ϊ ![]() ����Q����ȫ�������ʱ��Ϊ3s��
����Q����ȫ�������ʱ��Ϊ3s��
����������1��ֻҪ֤���ı���ȼ���֤������2������AE��CD��K����DE��AC��DE=OC=OA���Ƴ� ![]() =
= ![]() =
= ![]() ����AB=CD=6���ɵ�DK=2��CK=4����Rt��ADK�У�AK=
����AB=CD=6���ɵ�DK=2��CK=4����Rt��ADK�У�AK= ![]() =
= ![]() =3������sin��DAE=
=3������sin��DAE= ![]() ���㼴�ɽ�����⣻����PF��AD��F����֪PF=APsin��DAE=
���㼴�ɽ�����⣻����PF��AD��F����֪PF=APsin��DAE= ![]() AP����Ϊ��Q���˶�ʱ��t=
AP����Ϊ��Q���˶�ʱ��t= ![]() +
+ ![]() =OP+
=OP+ ![]() AP=OP+PF�����Ե�O��P��F����ʱ��OP+PF��ֵ��С����ʱOF�ǡ�ACD����λ�ߣ��ɴ˼��ɽ�����⣮
AP=OP+PF�����Ե�O��P��F����ʱ��OP+PF��ֵ��С����ʱOF�ǡ�ACD����λ�ߣ��ɴ˼��ɽ�����⣮
�����㾫����������Ҫ�����˹��ɶ����ĸ���;��ε����ʵ����֪ʶ�㣬��Ҫ����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����Ȳ�����ȷ�����⣮

����Ŀ�����ŵ������������ķ�չ�����������������ѳ�Ϊ�ܶ�������е�ѡ������Ļ���վ�������ȳ���������������ҽϽ���A��B��C��D��E�е�ijһվ�����������ﹲ�������ؼң�������������վ�����Ļ�������Ϊx(��λ��ǧ��)������������ʱ��y1(��λ������)�ǹ���x��һ�κ��������ϵ���±���
����վ | A | B | C | D | E |
x(ǧ��) | 8 | 9 | 10 | 11.5 | 13 |
y1(����) | 18 | 20 | 22 | 25 | 28 |
(1)��y1����x�ĺ�������ʽ��
(2)��ﵥ����ʱ��y2(��λ������)Ҳ��x��Ӱ�죬���ϵ������y2��![]() x2��11x��78�����������ʣ��Ӧѡ������һվ������������ʹ�����Ļ����ص��������ʱ����̣���������ʱ�䣮
x2��11x��78�����������ʣ��Ӧѡ������һվ������������ʹ�����Ļ����ص��������ʱ����̣���������ʱ�䣮