题目内容
(本题满分9分)将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图(1);再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF,如图2,证明:四边形AEDF是菱形.

略
解析:
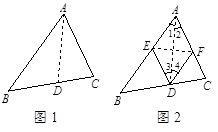
证明:由第一次折叠可知:AD为∠CAB的平分线,∴∠1=∠2……………………2分
由第二次折叠可知:∠CAB=∠EDF,从而,∠3=∠4………………………………4分
∵AD是△AED和△AFD的公共边,∴△AED≌△AFD(ASA)………………………6分
∴AE=AF,DE=DF
又由第二次折叠可知:AE=ED,AF=DF
∴AE=ED=DF=AF…………………………………………………………………………8分
故四边形AEDF是菱形.……………………………………………………………………9分

练习册系列答案
相关题目
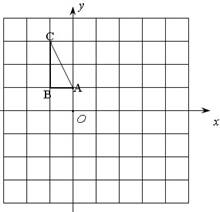
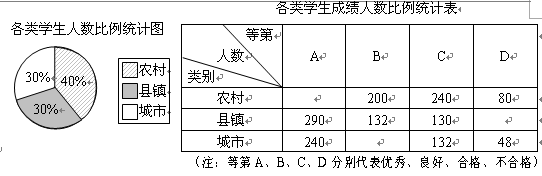

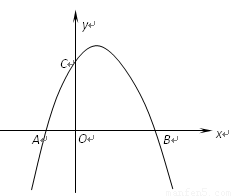
 恰好将平行四边形OABC的面积分成相等的两部分,试求b的值
恰好将平行四边形OABC的面积分成相等的两部分,试求b的值 轴、y轴的交点分别记为M、N,(1)中抛物线的对称轴与此抛物
轴、y轴的交点分别记为M、N,(1)中抛物线的对称轴与此抛物 ,
, ,
, ;图②中,
;图②中, ,
, ,
, .图③是刘卫同学所做的一个实验:他将
.图③是刘卫同学所做的一个实验:他将 的直角边
的直角边 与
与 的斜边
的斜边 重合在一起,并将
重合在一起,并将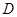 、
、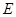 两点始终在
两点始终在 重合).
重合). 、
、 两点间的距离逐渐 ▲ .
两点间的距离逐渐 ▲ .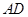 的长为多少时,
的长为多少时, 平行?
平行? 、
、 的长度为三边长的三角形是直角三角形?
的长度为三边长的三角形是直角三角形? ?如果存在,
?如果存在,


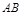 平移至
平移至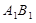 ,则
,则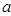 =
,
=
, =
。
=
。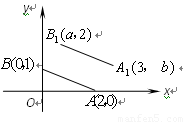
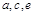 三者关系为
,
三者关系为
,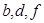 三者间关系为 。
三者间关系为 。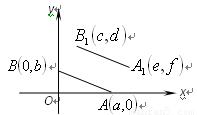
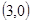 ,交y轴于C
,交y轴于C 点。
点。