��Ŀ����
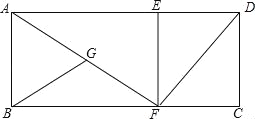
����Ŀ����ͼ���ھ���ABCD�У�AD=25��AB=12����E��F�ֱ���AD��BC�ϵĵ㣬��DE=CF=9������EF��DF��AF��ȡAF���е�ΪG������BG������BFG��BC����ƽ�ƣ�����F�����Cʱֹͣƽ�ƣ�Ȼ����GFB��C��˳ʱ����ת����0��������90�㣩���õ���B1CG1����G�Ķ�Ӧ��ΪG1����B�Ķ�Ӧ��ΪB1��������ת�����У�ֱ��B1G1��ֱ��EF��FD�ֱ��ཻM��N������FMN�ǵ��������Σ���FM=FNʱ���߶�DN�ij�Ϊ ��
���𰸡�![]() ��
��
��������
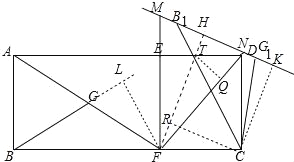
�����������ͼ����FL��BG��L��FH��MN��H��CK��MN��K��CR��FH��R��FH��ED��T����TQ��DF��Q��
���ı���ABCD�Ǿ��Σ�
���ABC=��ADC=��BCD=90�㣬AB=CD=12��AD=CF=25��
��DE=CF=9������DE��CF��
���ı���DEFC��ƽ���ı��Σ�
�ߡ�EDC=90�㣬
���ı���DEFC�Ǿ��Σ�ͬ���ı���AEFB�Ǿ��Σ�
��DF=![]() =15��AF=
=15��AF=![]() =20��
=20��
��AG=GF��
��S��BGF=![]() S��ABF=96=
S��ABF=96=![]() BGLF��
BGLF��
��FL=![]() ��
��
��CK=FL��
��CK=![]() ��
��
��FM=FN��FH��MN��CK��MN��CR��FH��
���RHK=��HKC=��KCR=90�㣬
���ı���RHKC�Ǿ��Σ�
��RH=CK=![]() ��
��
���MFH=��NFH��
��TE=TQ����TE=TQ=x��
��RT��TQD����TQ2+QD2=TD2��
��x2+32=��9-x��2��
��x=4��
��FT=![]() ��
��
�ߡ�EFT+��CFR=90�㣬��CFR+��FCR=90�㣬
���EFT=��FCR���ߡ�FET=��CFR=90�㣬
���FET�ס�CFR��
��![]() ��
��
��![]() ��
��
��RF=![]() ��
��
��FH=FR+RH=![]() ��
��
�ߡ�HFN=��HFM��
��cos��HFN=![]() ��
��
��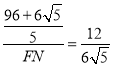 ��
��
��FN=![]() 3��
3��
��DN=FN-DF=![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�