题目内容
【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
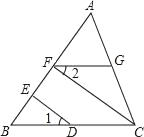
(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由;
(2)如图②,当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不须证明)
(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;
【答案】(1)AE=DF,AE⊥DF,理由详见解析;(2)是;(3)成立,理由详见解析.
【解析】
(1)AE=DF,AE⊥DF.先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;
(2)根据正方形性质得AD=DC,∠ADE=∠DCF=90°,DE=CF,可得△ADE≌△DCF,于是AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,故AE⊥DF;
(3)由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF;
(1)AE=DF,AE⊥DF.
理由:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠C=90°.
在△ADE和△DCF中,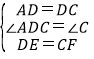 ,
,
∴△ADE≌△DCF(SAS).
∴AE=DF,∠DAE=∠CDF,
由于∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°.
∴AE⊥DF;
(2)是.四边形ABCD是正方形,所以AD=DC,∠ADE=∠DCF=90°,DE=CF,所以△ADE≌△DCF,于是AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,所以AE⊥DF;
(3)成立.
理由:由(1)同理可证AE=DF,∠DAE=∠CDF
延长FD交AE于点G,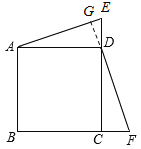
则∠CDF+∠ADG=90°,
∴∠ADG+∠DAE=90°.
∴AE⊥DF;

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案