题目内容
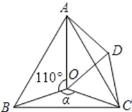
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
【答案】(1)见解析;(2)见解析;(3) 110°或125°或140°.
【解析】
(1)根据△BOC绕点C按顺时针方向旋转60°得△ADC,得CO=CD,∠OCD=60°故△COD是等边三角形;(2)求得∠ADO=∠ADC-∠CDO=90°即可知△AOD是直角三角形;(3)分别求出∠ADO=α-60°,∠AOD=360°-60°-110°-α=190°-α,再根据等腰三角形的底角相同分3中情况讨论.
解:(1)∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴∠ADC=∠BOC=α=150°,
∵△COD是等边三角形,
∴∠CDO=60°,
∴∠ADO=∠ADC-∠CDO=90°,
∴△AOD是直角三角形;
(3)∵△COD是等边三角形,
∴∠CDO=∠COD=60°,
∴∠ADO=α-60°,∠AOD=360°-60°-110°-α=190°-α,
当∠AOD=∠ADO时,△AOD是等腰三角形,即190°-α=α-60°,解得α=125°;
当∠AOD=∠DAO时,△AOD是等腰三角形,即2(190°-α)+α-60°=180°,解得α=140°;
当∠ADO=∠DAO时,△AOD是等腰三角形,即190°-α+2(α-60°)=180°,解得α=110°,
综上所述,∠BOC的度数为110°或125°或140°时,△AOD是等腰三角形.

【题目】在学校组织的知识竞赛活动中,老师将八年级一班和二班全部学生的成绩整理并绘制成如下统计表:
得分(分) 人数(人) 班级 | 50 | 60 | 70 | 80 | 90 | 100 |
一班 | 2 | 5 | 10 | 13 | 14 | 6 |
二班 | 4 | 4 | 16 | 2 | 12 | 12 |
(1)现已知一班和二班的平均分相同,请求出其平均分.
(2)请分别求出这两班的中位数和众数,并进一步分析这两个班级在这次竞赛中成绩的情况.