题目内容
【题目】如图,马戏团让狮子和公鸡表演跷跷板节目.跷跷板支柱 AB的高度为1.2米.
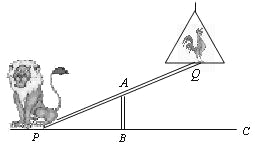
(1)若吊环高度为2米,支点 A为跷跷板 PQ的中点,狮子能否将公鸡送到吊环上?为什么?
(2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点 A移到跷跷板 PQ的什么位置时,狮子刚好能将公鸡送到吊环上?
【答案】(1)能;(2)支点 A移到跷跷板 PQ的三分之一处.
【解析】试题分析:
(1)如图,过点Q作QH⊥PC于点H,则由题意可得:AB∥QH,从而可得PB:BH=PA:AQ=1,说明AB是△PQH的中位线,则QH=2AB=2.4>2,故狮子能将公鸡送上吊环;
(2)由已知条件易得:△ PAB∽△ PQH,由此可得![]() ,说明当点A移到使AP=
,说明当点A移到使AP=![]() PQ处时,狮子刚好可将公鸡送到吊环上.
PQ处时,狮子刚好可将公鸡送到吊环上.
试题解析:
(1)狮子能将公鸡送到吊环上,理由如下:
如图,过点Q作QH⊥PC于点H,
∵AB⊥PC于点B,
∴AB∥QH,
∴PB:BH=PA:AQ=1,
∴AB是△PQH的中位线,
∴QH=2AB=2.4>2,
∴狮子能将公鸡送到吊环上;
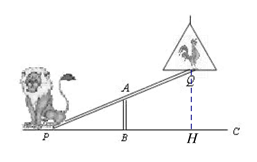
(2)由题意可知:QH=3.6,由(1)可知,AB∥QH,
∴△ PAB∽△ PQH,
∴![]() ,
,
∴PA=![]() PQ,即当点A在PQ上移动到使PA=
PQ,即当点A在PQ上移动到使PA=![]() PQ时,狮子刚好将公鸡送到吊环上.
PQ时,狮子刚好将公鸡送到吊环上.

练习册系列答案
相关题目