题目内容
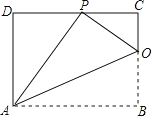
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于点O,连接AP、OP、OA.
(1)求证:![]() ;
;
(2)若△OCP与△PDA的面积比为1:4,求边AB的长.
【答案】(1)详见解析;(2)10.
【解析】
①只需证明两对对应角分别相等可得两个三角形相似;故![]() .
.
②根据相似三角形的性质求出PC长以及AP与OP的关系,然后在Rt△PCO中运用勾股定理求出OP长,从而求出AB长.
①∵四边形ABCD是矩形,
∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°.
由折叠可得:AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B.
∴∠APO=90°.
∴∠APD=90°∠CPO=∠POC.
∵∠D=∠C,∠APD=∠POC.
∴△OCP∽△PDA.
∴![]() .
.
②∵△OCP与△PDA的面积比为1:4,
∴OCPD=OPPA=CPDA=14√=12.
∴PD=2OC,PA=2OP,DA=2CP.
∵AD=8,
∴CP=4,BC=8.
设OP=x,则OB=x,CO=8x.
在△PCO中,
∵∠C=90,CP=4,OP=x,CO=8x,
∴x2=(8x)2+42.
解得:x=5.
∴AB=AP=2OP=10.
∴边AB的长为10.

练习册系列答案
相关题目