Question

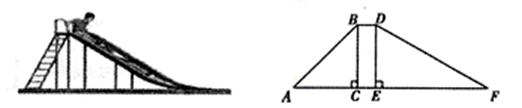
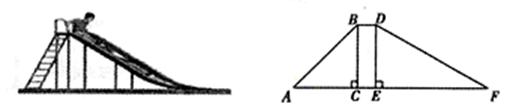
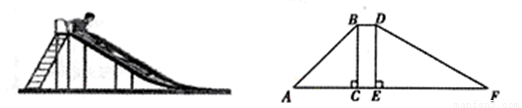
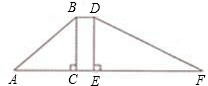
如图，在一滑梯侧面示意图中，BD∥AF，BC⊥AF与点C，DE⊥AF于点E，BC=1.8m，BD=0.5m，∠A=45°，∠F=29°
（1）求滑到DF的长（精确到0.1m）；
（2）求踏梯AB底端A与滑到DF底端F的距离AF（精确到0.1m）
（参考数据：sin29°≈0.48，cos29°≈0.87，tan29°≈0.55）

Answer 1

分析：（1）在Rt△DEF中，用正弦函数求解即可；
（2）分别在Rt△ABC、Rt△DEF中，通过解直角三角形求出AC、EF的长，进而由AF=AC+BD+EF求得AF的长．

解答：解：（1）在Rt△DEF中，∠DEF=90°，DE=BC=1.8，∠F=29°．
∵sinF=

DE

DF

，
∴DF=

DE

sinF

=

1.8

sin29°

≈

1.8

0.48

=3.75≈3.8．                    （3分）

（2）解法1：∵tanF=

DE

EF

，
∴EF=

DE

tanF

=

1.8

tan29°

≈

1.8

0.55

≈3.27．                         （2分）
在Rt△ABC中，∠ACB=90°，
∵∠A=45°，
∴AC=BC=1.8．
又∵CE=BD=0.5，
∴AF=AC+CE+EF≈1.8+0.5+3.27≈5.6．                         （2分）
解法2：∵cosF=

EF

DF

，
∴EF=DF•cos29°≈3.75×0.87≈3.26．                        （2分）
在Rt△ABC中，∠ACB=90°，
∵∠A=45°，∴AC=BC=1.8．
又∵CE=BD=0.5，
∴AF=AC+CE+EF≈1.8+0.5+3.26≈5.6．                         （2分）
答：DF长约为3.8m，AF约为5.6m．

点评：此题主要考查学生对坡度坡角的掌握及三角函数的运用能力．