题目内容
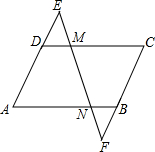 如图,直线EF分别交CD、AB于M、N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是
如图,直线EF分别交CD、AB于M、N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是
- A.∠A=∠C
- B.∠E=∠F
- C.AE∥FC
- D.AB∥DC
D
分析:因为∠EMD=65°,∠MNB=115°,所以∠EMD与∠MNB互补,则有AB∥DC,结合选项选择正确答案.
解答:∵∠EMD=65°,∠MNB=115°,
∴∠CMN=∠EMD=65°,
∴∠CMN+∠MNB=180°,
∴AB∥DC
故选D.
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
分析:因为∠EMD=65°,∠MNB=115°,所以∠EMD与∠MNB互补,则有AB∥DC,结合选项选择正确答案.
解答:∵∠EMD=65°,∠MNB=115°,
∴∠CMN=∠EMD=65°,
∴∠CMN+∠MNB=180°,
∴AB∥DC
故选D.
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.

练习册系列答案
相关题目
 26、如图,直线EF分别交AB、AC于F、E交BC延长线于D,已知AB•BF=DB•BC.求证:AE•CE=DE•EF.
26、如图,直线EF分别交AB、AC于F、E交BC延长线于D,已知AB•BF=DB•BC.求证:AE•CE=DE•EF.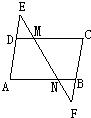 3、如图,直线EF分别交CD、AB于M、N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是( )
3、如图,直线EF分别交CD、AB于M、N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是( ) 5、如图,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=50°,∠2=70°,则下列结论正确的是( )
5、如图,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=50°,∠2=70°,则下列结论正确的是( ) 如图,直线EF分别交AB、CD于G、H.∠1=60°,∠2=120°,那么直线AB与CD的关系是
如图,直线EF分别交AB、CD于G、H.∠1=60°,∠2=120°,那么直线AB与CD的关系是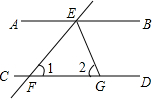 如图,直线EF分别交直线AB、CD于点E、F,EG平分∠BEF,若∠1=50°,∠2=65°,试判断直线AB与CD的位置关系,并说明理由.
如图,直线EF分别交直线AB、CD于点E、F,EG平分∠BEF,若∠1=50°,∠2=65°,试判断直线AB与CD的位置关系,并说明理由.