题目内容
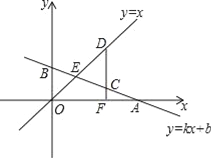
【题目】如图1所示,已知:点![]() 在双曲线
在双曲线![]() :
:![]() 上,直线
上,直线![]() ,直线
,直线![]() 与
与![]() 关于原点成中心对称,
关于原点成中心对称,![]() 两点间的连线与曲线
两点间的连线与曲线![]() 第一象限内的交点为
第一象限内的交点为![]() ,
,![]() 是曲线
是曲线![]() 上第一象限内异于
上第一象限内异于![]() 的一动点,过
的一动点,过![]() 作
作![]() 轴平行线分别交
轴平行线分别交![]() ,
,![]() 于
于![]() 两点.
两点.
(1)求双曲线![]() 及直线
及直线![]() 的解析式;
的解析式;
(2)求证:![]() ;
;
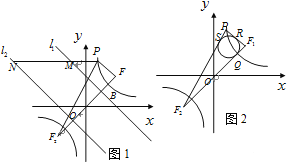
(3)如图2所示,![]() 的内切圆与
的内切圆与![]() 三边分别相切于点
三边分别相切于点![]() ,求证:点
,求证:点![]() 与点
与点![]() 重合.(参考公式:在平面坐标系中,若有点
重合.(参考公式:在平面坐标系中,若有点![]() ,
,![]() ,则A、B两点间的距离公式为=
,则A、B两点间的距离公式为=![]() .
.
【答案】(1)![]() ,
,![]() ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
试题分析:(1)把A点坐标代入![]() 可求得a值,即可得双曲线C的解析式,易得
可求得a值,即可得双曲线C的解析式,易得![]() 与
与![]() 轴的交点分别是
轴的交点分别是![]() ,可求得
,可求得![]() 与
与![]() 轴的交点关于原点对称点的坐标分别为
轴的交点关于原点对称点的坐标分别为![]() ,即可得直线
,即可得直线![]() 的解析式;(2)设
的解析式;(2)设![]() ,根据两点间的距离公式证明出
,根据两点间的距离公式证明出![]() ,
,![]() ,所以
,所以![]() ;(3)
;(3)![]() 与
与![]() 三别分别相切于点
三别分别相切于点![]() 所以PR=PS,
所以PR=PS,![]() ,
,![]() 可得
可得![]() ,又因
,又因![]() ,
,![]() 所以QO=2而
所以QO=2而![]() 即点
即点![]() 与点
与点![]() 重合.
重合.
试题解析:(1)解:![]()
![]() 与
与![]() 轴的交点分别是
轴的交点分别是![]() ,它们关于原点的对称点分别是
,它们关于原点的对称点分别是![]()
![]()
(2)设![]()
![]()
![]()
![]()
![]()
![]() ,
,
同理![]()
因此![]()
![]()
(3)![]() 与
与![]() 三别分别相切于点
三别分别相切于点![]()
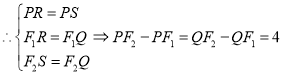
又![]() ,
,![]()
而![]()
所以,点![]() 与点
与点![]() 重合.(第三问如果计算得出
重合.(第三问如果计算得出![]() ,并且点
,并且点![]() 与点
与点![]() 都在线段
都在线段![]() 内,那么也可以证明点
内,那么也可以证明点![]() 与点
与点![]() 重合)
重合)

练习册系列答案
相关题目