Question

【题目】如图，抛物线y=过点C（4，3），交x轴于A，B两点（点A在点B的左侧）．

（1）求抛物线的解析式，并写出顶点M的坐标；

（2）连接OC，CM，求tan∠OCM的值；

（3）若点P在抛物线的对称轴上，连接BP，CP，BM，当∠CPB=∠PMB时，求点P的坐标．

Answer 1

【答案】(1) ，（2，﹣1）；(2)；(3) （2，2+）或（2，2﹣）．

【解析】

试题分析：（1）根据待定系数法，可得函数解析式；根据顶点式解析式，可得顶点坐标；

（2）根据勾股定理及逆定理，可得∠OMC=90°，根据正切函数，可得答案；

（3）根据相似三角形的判定与性质，可得PM的值，可得M点坐标．

试题解析：（1）由抛物线y=过点C（4，3），得

，解得a=1，

抛物线的解析式为，顶点M的坐标为（2，﹣1）；

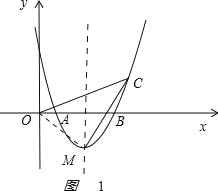
（2）如图1，

连接OM，==25，==5，==20，

∴+=，

∴∠OMC=90°，OM=，CM=，

tan∠OCM=；

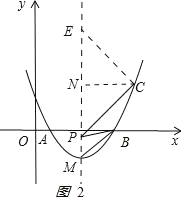
（3）如图2，

过C作CN⊥对称轴，垂足N在对称轴上，取一点E，使EN=CN=2，连接CE，EM=6．

当y=0时，，解得=1，=3，

∴A（1，0），B（3，0）．

由CN=EN，PB=PM，得

∠CEP=∠PMB=∠CPB=45°．

∵∠CPM=∠CEP+∠ECP，

∴∠ECP=∠BPM，

∴△CEP∽△PMB，

∴，解得MB=，CE=，

∴，解得PM=，

P点坐标为（2，2+）或（2，2﹣）．