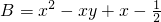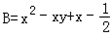Question

已知代数式A=2x²+3xy+2y-1，B=x2-xy+x-

1

2

（1）当x=y=-2时，求A-2B的值；
（2）若A-2B的值与x的取值无关，求y的值．

Answer 1

分析：（1）将A、B表示的代数式代入A-2B中，去括号，合并同类项即可；
（2）由（1）可知A-2B=5xy+2y-2x，将含x的项合并得（5y-2）x+2y，令含xd的项系数为0即可．

解答：解：（1）A-2B=2x²+3xy+2y-1-2（x2-xy+x-

1

2

）
=2x²+3xy+2y-1-2x²+2xy-2x+1
=5xy+2y-2x，
当x=y=-2时，
A-2B=5xy+2y-2x
=5×（-2）×（-2）+2×（-2）-2×（-2）
=20；

（2）由（1）可知A-2B=5xy+2y-2x=（5y-2）x+2y，
若A-2B的值与x的取值无关，则5y-2=0，
解得y=

2

5

．

点评：本题考查了整式的化简．整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．