题目内容
矩形的对角线长为8cm,则依次连接矩形各边中点得到的四边形的周长为
- A.8cm
- B.12cm
- C.16cm
- D.20cm
C
分析:根据三角形中位线定理,易得出所得四边形的两组对边的和正好等于矩形的两条对角线长,由此得到所求的结论.
解答: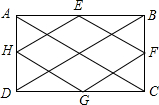 解:如图;
解:如图;
矩形ABCD中,E、F、G、H分别是四边的中点;
由三角形中位线定理知:AC=2EF=2HG,BD=2HG=2EF;
∴四边形EFGH的周长=EF+HG+EH+GF=AC+BD=16cm;
故选C.
点评:此题主要考查的是矩形的性质以及三角形中位线定理的综合应用.
分析:根据三角形中位线定理,易得出所得四边形的两组对边的和正好等于矩形的两条对角线长,由此得到所求的结论.
解答:
 解:如图;
解:如图;矩形ABCD中,E、F、G、H分别是四边的中点;
由三角形中位线定理知:AC=2EF=2HG,BD=2HG=2EF;
∴四边形EFGH的周长=EF+HG+EH+GF=AC+BD=16cm;
故选C.
点评:此题主要考查的是矩形的性质以及三角形中位线定理的综合应用.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目