题目内容
已知函数y1=ax2+bx+c(a≠0)和y2=mx+n的图象交于(-2,-5)点和(1,4)点,并且y1=ax2+bx+c的图象与y轴交于点(0,3).
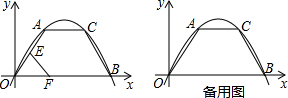
(1)求函数y1和y2的解析式,并画出函数示意图;
(2)x为何值时,①y1>y2;②y1=y2;③y1<y2.

(1)求函数y1和y2的解析式,并画出函数示意图;
(2)x为何值时,①y1>y2;②y1=y2;③y1<y2.

(1)把(-2,-5)、(1,4)、(0,3)代入y1=ax2+bx+c(a≠0)得
,
解得
,
所以y1=-x2+2x+3,
把(-2,-5)、(1,4)代入y2=mx+n得
,
解得
,
所以y2=3x+1;如图
(2)①当-2<x<1时,y1>y2.
②当x=-2或x=1时,y1=y2.
③当x<-2或x>1时y1<y2.

|
解得
|
所以y1=-x2+2x+3,
把(-2,-5)、(1,4)代入y2=mx+n得
|
解得
|
所以y2=3x+1;如图
(2)①当-2<x<1时,y1>y2.
②当x=-2或x=1时,y1=y2.
③当x<-2或x>1时y1<y2.


练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
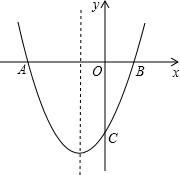
 男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).
男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).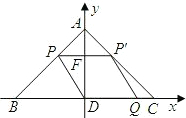 向作匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为y,DQ=x.
向作匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为y,DQ=x.