题目内容
【题目】平面内的两条直线有相交和平行两种位置关系．
（1）如图1，若AB∥CD，点P在AB，CD内部，∠B=50°，∠D=30°，求∠BPD．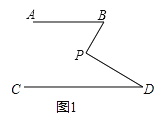 
（2）如图2，将点P移到AB，CD外部，则∠BPD，∠B，∠D之间有何数量关系？请证明你的结论．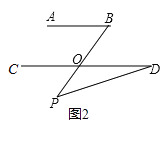 
（3）如图3，写出∠BPD，∠B，∠D，∠BQD之间的数量关系？（不需证明）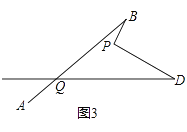 
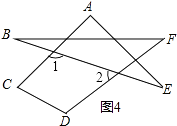
（4）如图4，求出∠A+∠B+∠C+∠D+∠E+∠F的度数．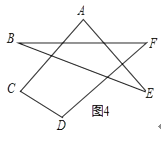 
【答案】
（1）解：过点P作PE∥AB，
∵AB∥CD，
∴AB∥EP∥CD，
∴∠B=∠1=50°，∠D=∠2=30°，
∴∠BPD=80°
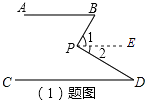
（2）解：∠B=∠BPD+∠D．
理由如下：设BP与CD相交于点O，
∵AB∥CD，
∴∠BOD=∠B，
在△POD中，∠BOD=∠BPD+∠D，
∴∠B=∠BPD+∠D
（3）解：如图，连接QP并延长，
结论：∠BPD=∠BQD+∠B+∠D
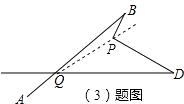
（4）解：如图，由三角形的外角性质，∠A+∠E=∠1，∠B+∠F=∠2，
∵∠1+∠2+∠C+∠D=360°，
∴∠A+∠B+∠C+∠D+∠E+∠F=360°．
【解析】（1）过点P作PE∥AB，根据两直线平行，内错角相等可得∠B=∠1，∠D=∠2，再根据∠BPD=∠1+∠2代入数据计算即可得解；（2）根据根据两直线平行，内错角相等可得∠BOD=∠B，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式整理即可得解；（3）连接QP并延长，再根据三角形的一个外角等于与它不相邻的两个内角的和解答；（4）根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠E=∠1，∠B+∠F=∠2，再根据四边形的内角和定理列式计算即可得解．
【考点精析】认真审题，首先需要了解平行线的性质(两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补)，还要掌握三角形的内角和外角(三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键．
