题目内容
(2002•黄石)如图,已知△ABC中,AB=AC=13cm,BC=10cm,以AB为直径作⊙O交BC于D,交AC于E.过D作DF⊥AC,垂足为F.(1)求证:DF是⊙O的切线;
(2)求四边形ABDE的面积.

【答案】分析:(1)连接AD、OD,则AD⊥BC,D为BC中点.OD为中位线,则OD∥AC,根据DF⊥AC可得OD⊥DF.得证;
(2)S四边形ABDE=S△ABC-S△DCE.易求S△ABC,关键求S△DCE.根据切割线定理可求CE;根据等积法可求DF.则可求S△DCE.
解答: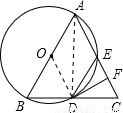 (1)证明:连接AD.
(1)证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC.
又AB=AC=13,BC=10,D是BC的中点,
∴BD=5.
连接OD;
由中位线定理,知DO∥AC,
又DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线.
(2)解:由割线定理,得CE•CA=CD•CB,即
CE×13=5×10,得CE=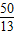 .
.
∵S△ACD= AD•DC=
AD•DC= AC•DF,即13•DF=12×5,
AC•DF,即13•DF=12×5,
∴DF=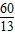 ,
,
∴S四边形ABDE=S△ABC-S△DCE= ×10×12-
×10×12- ×
×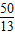 ×
×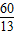 =
=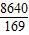 .
.
点评:此题考查了切线的判定、图形的面积计算等知识点,难度中等.
(2)S四边形ABDE=S△ABC-S△DCE.易求S△ABC,关键求S△DCE.根据切割线定理可求CE;根据等积法可求DF.则可求S△DCE.
解答:
 (1)证明:连接AD.
(1)证明:连接AD.∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC.
又AB=AC=13,BC=10,D是BC的中点,
∴BD=5.
连接OD;
由中位线定理,知DO∥AC,
又DF⊥AC,
∴DF⊥OD.
∴DF是⊙O的切线.
(2)解:由割线定理,得CE•CA=CD•CB,即
CE×13=5×10,得CE=
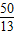 .
.∵S△ACD=
 AD•DC=
AD•DC= AC•DF,即13•DF=12×5,
AC•DF,即13•DF=12×5,∴DF=
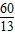 ,
,∴S四边形ABDE=S△ABC-S△DCE=
 ×10×12-
×10×12- ×
×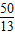 ×
×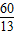 =
=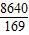 .
.点评:此题考查了切线的判定、图形的面积计算等知识点,难度中等.

练习册系列答案
相关题目

 ,
, )的切线交x轴于A点,交y轴于B点.
)的切线交x轴于A点,交y轴于B点.
 ,
, )的切线交x轴于A点,交y轴于B点.
)的切线交x轴于A点,交y轴于B点.
