题目内容
 如图:折叠长方形ABCD(四个角都是直角,对边相等)的一边AD,点D落在BC边的F处,已知AB=8cm,BC=10cm,则EC=
如图:折叠长方形ABCD(四个角都是直角,对边相等)的一边AD,点D落在BC边的F处,已知AB=8cm,BC=10cm,则EC=分析:利用勾股定理可得BF的长,也就求得了FC的长,进而利用勾股定理可得EC的长.
解答:解:由折叠可知:AF=AD=BC=10,DE=EF.
∵AB=8,
∴BF=
=6,
∴FC=4,EF=ED=8-EC,
在Rt△EFC中,
EC2+FC2=EF2,即EC2+42=(8-EC)2,
解得EC=3.
故答案为:3cm.
∵AB=8,
∴BF=
| AF2-AB2 |
∴FC=4,EF=ED=8-EC,
在Rt△EFC中,
EC2+FC2=EF2,即EC2+42=(8-EC)2,
解得EC=3.
故答案为:3cm.
点评:考查有关折叠问题的应用;利用两次勾股定理得到所需线段长是解决本题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
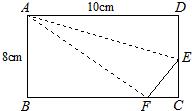 15、如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求:(1)FC的长;(2)EF的长.
15、如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,求:(1)FC的长;(2)EF的长.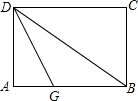 如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,再折叠使AD边与BD重合,得折痕DG,若AB=4,BC=3,求AG的长.
如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,再折叠使AD边与BD重合,得折痕DG,若AB=4,BC=3,求AG的长.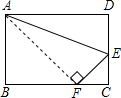 如图,折叠长方形,使点D落在BC边上的点F处,BC=10cm,AB=8cm,求EF的长.
如图,折叠长方形,使点D落在BC边上的点F处,BC=10cm,AB=8cm,求EF的长.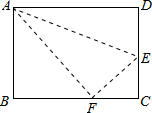 如图,折叠长方形ABCD的一边AD,使点D落在BC边上的F处,己知AB=8cm,BC=10cm,求折痕AE的长.
如图,折叠长方形ABCD的一边AD,使点D落在BC边上的F处,己知AB=8cm,BC=10cm,求折痕AE的长.