题目内容
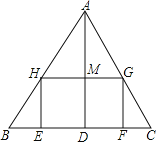
【题目】如图，△ABC是一张锐角三角形的硬纸片．AD是边BC上的高，BC=40cm，AD=30cm．从这张硬纸片剪下一个长HG是宽HE的2倍的矩形EFGH．使它的一边EF在BC上，顶点G，H分别在AC，AB上．AD与HG的交点为M．
（1）求证：
；
（2）求这个矩形EFGH的周长．
【答案】（1）证明见解析；（2）72cm．
【解析】
（1）根据矩形性质得出∠AHG=∠ABC，再证明△AHG∽△ABC，即可得出结论；
（2）根据（1）中比例式即可求出HE的长度，以及矩形的周长．
解：（1）证明：∵四边形EFGH为矩形，
∴EF∥GH，
∴∠AHG=∠ABC，
又∵∠HAG=∠BAC，
∴△AHG∽△ABC，
∴
；
（2）解：由（1）得：设HE=xcm，则MD=HE=xcm．
∵AD=30cm，
∴AM=（30﹣x）cm．
∵HG=2HE，
∴HG=（2x）cm，
可得：
，
解得：x=12，
故HG=2x=24，
所以矩形EFGH的周长为：2×（12+24）=72（cm）．
答：矩形EFGH的周长为72cm．
全优测试卷系列答案
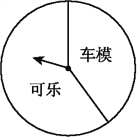
冲刺100分1号卷系列答案
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
