题目内容
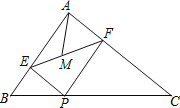
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .
【答案】![]()
【解析】
试题分析:根据矩形的性质就可以得出EF,AP互相平分,且EF=AP,根据垂线段最短的性质就可以得出AP⊥BC时,AP的值最小,即AM的值最小,由勾股定理求出BC,根据面积关系建立等式求出其解即可.
解:∵PE⊥AB,PF⊥AC,∠BAC=90°,
∴∠EAF=∠AEP=∠AFP=90°,
∴四边形AEPF是矩形,
∴EF,AP互相平分.且EF=AP,
∴EF,AP的交点就是M点,
∵当AP的值最小时,AM的值就最小,
∴当AP⊥BC时,AP的值最小,即AM的值最小.
∵![]() AP×BC=
AP×BC=![]() AB×AC,
AB×AC,
∴AP×BC=AB×AC,
在Rt△ABC中,由勾股定理,得BC=![]() =10,
=10,
∵AB=6,AC=8,
∴10AP=6×8,
∴AP=![]()
∴AM=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
