Question

如图，点D、E是△ABC边AB、AC上的两点，DE∥BC，延长DE至F，使DF=BC．若AD=x，DB=3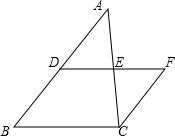，DE=2，EF=y．
（1）求y与x之间的函数关系式．
（2）当EF=3时，求AB的长．

Answer 1

分析：（1）根据DE∥BC，延长DE至F，使DF=BC，证明△ADE∽△CFE，再用对应边成比例即可解题．
（2）将EF=3时代入则y=

6

x

，即可求得AB的长．

解答：解：（1）∵DE∥BC，延长DE至F，使DF=BC，
∴DBCF是平行四边形，AB∥CF，BD=CF
∴△ADE∽△CFE，∴

AD

CF

=

DE

EF

，即

x

3

=

2

y

，
则y=

6

x

．
答：（1）y与x之间的函数关系式为：y=

6

x

．

（2）将EF=3时代入则y=

6

x

，则x=2，即AD=2，
AB=AD+DB=2+3=5．
答：（2）当EF=3时，AB的长是5．

点评：此题主要考查学生对相似三角形的判定与性质，和平行四边形的判定与性质的理解和掌握．难度不大，是一道基础题．