题目内容
根据实际问题的意义列出方程:
一批树苗按下列方法依次由各班领取:第一班取10棵和余下的
,第二班取20棵和余下的
,第三班取30棵和余下的
,…,最后树苗全部被取完,且各班的树苗数都相等,求树苗总数.(只列方程,不求解)
一批树苗按下列方法依次由各班领取:第一班取10棵和余下的
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
分析:设树苗总数为x棵,根据各班的树苗数都相等,可得出第一班和第二班领取的树苗数相等,由此可得出方程.
解答:解:设树苗总数为x棵,
则第一班领取的树苗数量为:10+
(x-10),
第二班领取的树苗数量为:20+
{x-20-[10+
(x-10)]},
∵各班的树苗数都相等,
∴可得10+
(x-10)=20+
{x-20-[10+
(x-10)]}.
则第一班领取的树苗数量为:10+
| 1 |
| 10 |
第二班领取的树苗数量为:20+
| 1 |
| 10 |
| 1 |
| 10 |
∵各班的树苗数都相等,
∴可得10+
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |
点评:本题考查了由实际问题抽象一元一次方程的知识,解答本题的关键是得出各班的树苗数都相等,这个等量关系,因为第一班,第二班领取数量好表示,所以我们就选取这两班建立等量关系.

练习册系列答案
相关题目
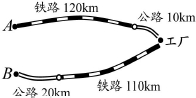 费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元?
费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元? ,第二班取20棵和余下的
,第二班取20棵和余下的