题目内容
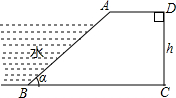
如图，在菱形ABCD中，AE⊥BC，E为垂足，若cosB=
，EC=2，P是AB边上的一个动点，则线段PE的长度的最小值是______．
| 4 |
| 5 |
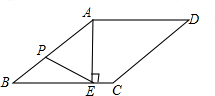
设菱形ABCD的边长为x，则AB=BC=x，又EC=2，所以BE=x-2，
因为AE⊥BC于E，
所以在Rt△ABE中，cosB=
，又cosB=
，
于是
=
，
解得x=10，即AB=10．
所以易求BE=8，AE=6，
当EP⊥AB时，PE取得最小值．
故由三角形面积公式有：
AB•PE=
BE•AE，
求得PE的最小值为4.8．
故答案为 4.8．
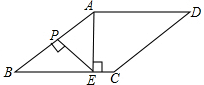
因为AE⊥BC于E，
所以在Rt△ABE中，cosB=
| x-2 |
| x |
| 4 |
| 5 |
于是
| x-2 |
| x |
| 4 |
| 5 |
解得x=10，即AB=10．
所以易求BE=8，AE=6，
当EP⊥AB时，PE取得最小值．
故由三角形面积公式有：
| 1 |
| 2 |
| 1 |
| 2 |
求得PE的最小值为4.8．
故答案为 4.8．
练习册系列答案
名校课堂系列答案
相关题目
