题目内容
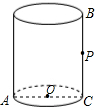如图，圆柱的底面周长为12cm，AC是底面圆的直径，高BC=10cm，点P是BC上一点且PC=| 4 |
| 5 |
| A、9cm | B、10cm |
| C、11cm | D、12cm |
分析：先把图形展开，连接AP，求出CP、AC长，根据勾股定理求出AP即可．
解答：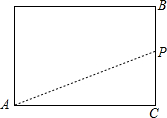
解：如图展开，连接AP，则线段AP的长是从A点出发沿着圆柱的表面爬行到点P的最短距离，
∵BC=10cm，PC=
BC，
∴PC=8cm，
∵圆柱的底面周长为12cm，
∴AC=6cm，
在Rt△ACP中，由勾股定理得：AP=
=10（cm），
故选B．
解：如图展开，连接AP，则线段AP的长是从A点出发沿着圆柱的表面爬行到点P的最短距离，
∵BC=10cm，PC=
| 4 |
| 5 |
∴PC=8cm，
∵圆柱的底面周长为12cm，
∴AC=6cm，
在Rt△ACP中，由勾股定理得：AP=
| 62+82 |
故选B．
点评：此题考查了几何体的展开图的应用，以及线段的性质：两点之间线段最短，解决立体几何两点间的最短距离时，通常把立体图形展开成平面图形，转化成平面图形两点间的距离问题来求解．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
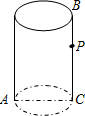如图，圆柱的底面周长为6cm，AC是底面圆的直径，高BC=6cm，点P是母线BC上一点，且PC=| 2 |
| 3 |
A、(4+
| ||
| B、5cm | ||
C、3
| ||
| D、7cm |
BC．一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是（ ）
㎝ 
㎝