题目内容
如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系,请证明你的猜想;
(2)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系还成立吗?若成立,给出证明;若不成立,请说明理由;
(3)若AC=BC=4,设△EFP平移的距离为x,当0≤x≤8时,△EFP与△ABC重叠部分的面积为S,请写出S与x之间的函数关系式,并求出最大值.
分析:(1)根据图形就可以猜想出结论.
(2)要证BQ=AP,可以转化为证明△BCQ≌△ACP得出BQ=AP;
(3)设△EFP平移的距离为x,当0≤x<4时,S=-
x2+4x,当4≤x≤8时,S=
x(x-8)2,解得x即可.
(2)要证BQ=AP,可以转化为证明△BCQ≌△ACP得出BQ=AP;
(3)设△EFP平移的距离为x,当0≤x<4时,S=-
| 3 |
| 4 |
| 1 |
| 4 |
解答:解:(1)猜想:BQ=AP.
证明:由题意可知EF⊥FP,又EF=FP,
所以∠EPF=45°,
所以QC=CP,又∠BCQ=∠ACP=90°,AC=BC,
所以△BCQ≌△ACP,
得出BQ=AP;
(2)BQ=AP.
证明:∵∠EPF=45°,AC⊥CP,
∴CQ=CP,
又∵BC=AC,
∴Rt△BCQ≌Rt△ACP,
∴BQ=AP;
(3)当0≤x<4时,S=-
x2+4x,
当4≤x≤8时,S=
x(x-8)2,
当0≤x<4时,x=-
=
时,S的最大值为
;
当4≤x≤8时,根据对称轴左侧y随x的增大而减小,
∴x=4时,S的最大值为4.
∴当x=
时,S的最大值为
.
证明:由题意可知EF⊥FP,又EF=FP,
所以∠EPF=45°,
所以QC=CP,又∠BCQ=∠ACP=90°,AC=BC,
所以△BCQ≌△ACP,
得出BQ=AP;
(2)BQ=AP.
证明:∵∠EPF=45°,AC⊥CP,
∴CQ=CP,
又∵BC=AC,
∴Rt△BCQ≌Rt△ACP,
∴BQ=AP;
(3)当0≤x<4时,S=-
| 3 |
| 4 |
当4≤x≤8时,S=
| 1 |
| 4 |
当0≤x<4时,x=-
| b |
| 2a |
| 8 |
| 3 |
| 16 |
| 3 |
当4≤x≤8时,根据对称轴左侧y随x的增大而减小,
∴x=4时,S的最大值为4.
∴当x=
| 8 |
| 3 |
| 16 |
| 3 |
点评:此题主要考查全等三角形的判定与性质,等腰三角形的性质,平移的性质,二次函数的最值等知识点,证明两个线段相等可以转化为证明三角形全等的问题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
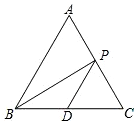 如图,正三角形ABC的边长为a,D是BC的中点,P是AC边上的点,连接PB和PD得到△PBD.求:
如图,正三角形ABC的边长为a,D是BC的中点,P是AC边上的点,连接PB和PD得到△PBD.求: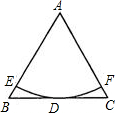 如图,正△ABC的边长AB=2,以A为圆心的圆切BC于点D,交AB于点E,交AC于点F,则弧EF的长=
如图,正△ABC的边长AB=2,以A为圆心的圆切BC于点D,交AB于点E,交AC于点F,则弧EF的长=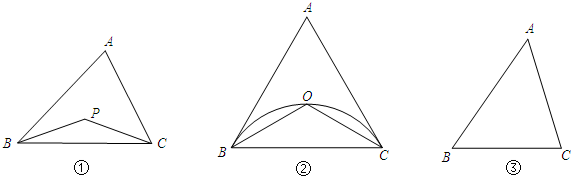
 如图,以△ABC的边AB、AC向外作等边△ABE和△ACD,连接BD、CE.
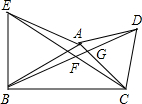
如图,以△ABC的边AB、AC向外作等边△ABE和△ACD,连接BD、CE.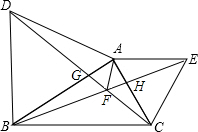 如图,以△ABC的边AB、AC为边,向外作等边△ABD和等边△ACE,连接BE、CD相交于点F.
如图,以△ABC的边AB、AC为边,向外作等边△ABD和等边△ACE,连接BE、CD相交于点F.