题目内容
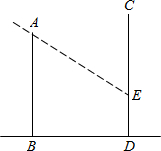 如图,甲楼AB高18m,乙楼CD坐落在甲楼的正东面,已知当地冬至中午12时,物高与影长的比是1:
如图,甲楼AB高18m,乙楼CD坐落在甲楼的正东面,已知当地冬至中午12时,物高与影长的比是1:| 2 |
分析:设FE⊥AB于点F,那么在△AEF中,∠AFE=90°,解直角三角形AEC可以求得AF的长,进而求得DE=AB-AF即可解题.
解答: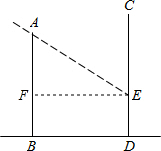 解:设冬天太阳最低时,甲楼最高处A点的影子落在乙楼的E处,那么图中ED的长度就是甲楼的影子在乙楼上的高度,
解:设冬天太阳最低时,甲楼最高处A点的影子落在乙楼的E处,那么图中ED的长度就是甲楼的影子在乙楼上的高度,
设FE⊥AB于点F,那么在△AEF中,∠AFE=90°,EF=20米.
∵物高与影长的比是1:
,
∴
=
,
则AF=
EF=10
,
故DE=FB=18-10
.
答:甲楼的影子落在乙楼上有18-10
m.
 解:设冬天太阳最低时,甲楼最高处A点的影子落在乙楼的E处,那么图中ED的长度就是甲楼的影子在乙楼上的高度,
解:设冬天太阳最低时,甲楼最高处A点的影子落在乙楼的E处,那么图中ED的长度就是甲楼的影子在乙楼上的高度,设FE⊥AB于点F,那么在△AEF中,∠AFE=90°,EF=20米.
∵物高与影长的比是1:
| 2 |
∴
| AF |
| EF |
| 1 | ||
|
则AF=
| ||
| 2 |
| 2 |
故DE=FB=18-10
| 2 |
答:甲楼的影子落在乙楼上有18-10
| 2 |
点评:本题考查了相似三角似三角形的应用和特殊角的三角函数值,根据物高与影长的比是1:
,得出AF的值是解题的关键.
| 2 |

练习册系列答案
相关题目
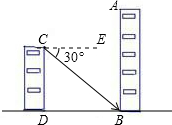 如图,小明家居住的甲楼AB面向正北,现计划在他家居住的楼前修建一座乙楼CD,楼高为18米,已知冬天的太阳最低时,光线与水平线的夹角为30°,若让乙楼的影子刚好不影响甲楼,则两楼之间距离至少应是多少米?
如图,小明家居住的甲楼AB面向正北,现计划在他家居住的楼前修建一座乙楼CD,楼高为18米,已知冬天的太阳最低时,光线与水平线的夹角为30°,若让乙楼的影子刚好不影响甲楼,则两楼之间距离至少应是多少米?  =
= 如图,小明家居住的甲楼AB面向正北,现计划在他家居住的楼前修建一座乙楼CD,楼高为18米,已知冬天的太阳最低时,光线与水平线的夹角为30°,若让乙楼的影子刚好不影响甲楼,则两楼之间距离至少应是多少米?
如图,小明家居住的甲楼AB面向正北,现计划在他家居住的楼前修建一座乙楼CD,楼高为18米,已知冬天的太阳最低时,光线与水平线的夹角为30°,若让乙楼的影子刚好不影响甲楼,则两楼之间距离至少应是多少米?
 ,cos37°=
,cos37°= ,tan37°=
,tan37°= )
)