题目内容
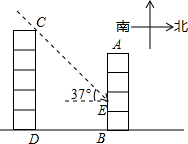
小强家居住在甲楼AB,面向正南.某房地产商计划在他家居住的楼前修建一座高为18米的乙楼CD,两楼之间的距离为20米.已知冬天的一段时间里,太阳光线与水平线的夹角为37°(如图).(备用数据:sin37°= ,cos37°=
,cos37°= ,tan37°=
,tan37°= )
)(1)试求乙楼CD的影子落在甲楼AB上的高BE的长;
(2)若让乙楼的影子刚好不影响甲楼,则两楼之间的距离至少应为多少米?
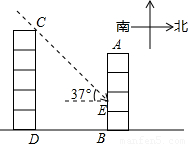
【答案】分析:(1)过点E作EF∥BD交CD于点F,利用EF=BD=20,∠CFE=90°求得线段EF的长,然后利用BE=DF=CD-CF=3求得BE的长即可.
(2)延长CE交直线DB于点G,利用∠CGD的正切值求得线段CD的长,进而可以求得线段BG的长,即可求得两楼之间的距离的最小值.
解答: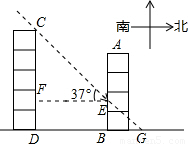 (1)过点E作EF∥BD交CD于点F,
(1)过点E作EF∥BD交CD于点F,
则EF=BD=20,∠CFE=90°
∴tan∠CEF=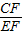
又∠CEF=37°tan37°=
∴CF=15
∴从而BE=DF=CD-CF=3.
(2)延长CE交直线DB于点G,
则∠CGD=37°,∠CDG=90°
∴tan∠CGD=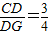
又CD=18
∴DG=24
∴两楼之间的距离至少应为24米.(12分)
点评:本题考查了解直角三角形的应用,解题的关键是正确的从中整理出直角三角形模型,利用解直角三角形的知识求相应的线段的长即可.
(2)延长CE交直线DB于点G,利用∠CGD的正切值求得线段CD的长,进而可以求得线段BG的长,即可求得两楼之间的距离的最小值.
解答:
 (1)过点E作EF∥BD交CD于点F,
(1)过点E作EF∥BD交CD于点F,则EF=BD=20,∠CFE=90°
∴tan∠CEF=
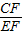
又∠CEF=37°tan37°=

∴CF=15
∴从而BE=DF=CD-CF=3.
(2)延长CE交直线DB于点G,
则∠CGD=37°,∠CDG=90°
∴tan∠CGD=
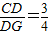
又CD=18
∴DG=24
∴两楼之间的距离至少应为24米.(12分)
点评:本题考查了解直角三角形的应用,解题的关键是正确的从中整理出直角三角形模型,利用解直角三角形的知识求相应的线段的长即可.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 =
= =
= ,cos37°=
,cos37°= ,tan37°=
,tan37°= )
)