题目内容
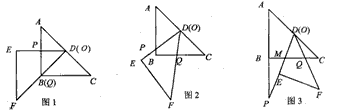
如图所示，将直角三角形ACB，∠C=90°，AC=6，沿CB方向平移得直角三角形DEF，BF=2，DG=
，阴影部分面积为________．
10.5
分析：根据平移的性质，对应点间的距离等于平移的距离求出CE=BF，再求出GE，然后根据平移变换只改变图形的位置不改变图形的形状与大小可得△ABC的面积等于△DEF的面积，从而得到阴影部分的面积等于梯形ACEG的面积，再利用梯形的面积公式列式计算即可得解．
解答：∵△ACB平移得到△DEF，
∴CE=BF=2，DE=AC=6，
∴GE=DE-DG=6-=4.5，
由平移的性质，S△ABC=S△DEF，
∴阴影部分的面积=S梯形ACEG=
（GE+AC）•CE=（4.5+6）×2=10.5．
故答案为：10.5．
点评：本题考查了平移的性质，熟练掌握性质并求出阴影部分的面积等于梯形ACEG的面积是本题的难点，也是解题的关键．
分析：根据平移的性质，对应点间的距离等于平移的距离求出CE=BF，再求出GE，然后根据平移变换只改变图形的位置不改变图形的形状与大小可得△ABC的面积等于△DEF的面积，从而得到阴影部分的面积等于梯形ACEG的面积，再利用梯形的面积公式列式计算即可得解．
解答：∵△ACB平移得到△DEF，
∴CE=BF=2，DE=AC=6，
∴GE=DE-DG=6-
=4.5，由平移的性质，S△ABC=S△DEF，
∴阴影部分的面积=S梯形ACEG=
（GE+AC）•CE=（4.5+6）×2=10.5．故答案为：10.5．
点评：本题考查了平移的性质，熟练掌握性质并求出阴影部分的面积等于梯形ACEG的面积是本题的难点，也是解题的关键．
练习册系列答案
相关题目
