题目内容
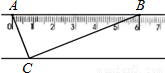
已知:如图,直尺的宽度为2,A、B两点在直尺的一条边上,AB=6,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为 .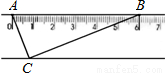
【答案】分析:由∠ACB=∠ADB=90°,根据90°的圆周角所对的弦是直径,可得A,B,C,D在以AB为直径的圆上,C,D即是此圆与直尺的交点,设E为AB中点,可得EC是半径为3,然后作EF⊥CD交CD于F,根据垂径定理可得:CD=2CF,然后由勾股定理求得CF的长,继而求得答案.
解答: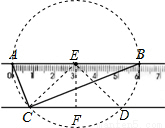 解:设E为AB中点,
解:设E为AB中点,
∵∠ACB=∠ADB=90°,
∴A,B,C,D在以AB为直径的圆上,
连接DE,CE,则CE=DE= AB=3,
AB=3,
作EF⊥CD交CD于F,
∴CD=2CF,
∵AB∥CD,
∴EF=2,
在Rt△CFE和Rt△DFE中,CF=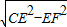 =
=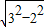 =
=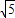 ,
,
∴CD=2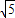 .
.
故答案为:2 .
.
点评:此题考查了圆周角定理,垂径定理以及勾股定理等知识.此题拿度适中,解题的关键是由∠ACB=∠ADB=90°,根据90°的圆周角所对的弦是直径,得到A,B,C,D在以AB为直径的圆上.
解答:
 解:设E为AB中点,
解:设E为AB中点,∵∠ACB=∠ADB=90°,
∴A,B,C,D在以AB为直径的圆上,
连接DE,CE,则CE=DE=
 AB=3,
AB=3,作EF⊥CD交CD于F,
∴CD=2CF,
∵AB∥CD,
∴EF=2,
在Rt△CFE和Rt△DFE中,CF=
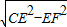 =
=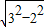 =
=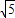 ,
,∴CD=2
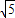 .
.故答案为:2
 .
.点评:此题考查了圆周角定理,垂径定理以及勾股定理等知识.此题拿度适中,解题的关键是由∠ACB=∠ADB=90°,根据90°的圆周角所对的弦是直径,得到A,B,C,D在以AB为直径的圆上.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 (2007•海淀区二模)已知:如图,直尺的宽度为2,A、B两点在直尺的一条边上,AB=6,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为
(2007•海淀区二模)已知:如图,直尺的宽度为2,A、B两点在直尺的一条边上,AB=6,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为
 已知:如图,直尺的宽度为2,A、B两点在直尺的一条边上,AB=6,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为________.
已知:如图,直尺的宽度为2,A、B两点在直尺的一条边上,AB=6,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为________.