��Ŀ����
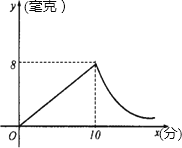
����Ŀ��ijУ������Ա�μ���ṫ����������һ����Ըƿ�������ۣ������������������ƻ���.�����г����飬������Ըƿһ��ʱ���ڵ�������y�����������۵���x��Ԫ/����֮��Ķ�Ӧ��ϵ��ͼ��ʾ��
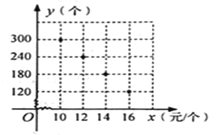
��1�����ж�y��x֮��ĺ�����ϵ�������������ϵʽ��
��2������Ըƿ�Ľ���Ϊ6Ԫ/�������������г���������۹��ɣ�����������w��Ԫ�������۵���x��Ԫ/����֮��ĺ�����ϵʽ��
��3���ڣ�2���������£�����Ըƿ�Ľ����ɱ�������900Ԫ��Ҫ��������������ȷ��������Ըƿ�����۵��ۣ��������ʱ���������.
���𰸡���1��y=-30x+600����2��![]() ����3��x=15ʱ���������1350Ԫ.
����3��x=15ʱ���������1350Ԫ.
��������
���⣨1���۲�ɵøú���ͼ����һ�κ��������һ�κ�������ʽ��������������뼴����øú�������ʽ����������������ĺ�������뿴�������Ƿ�������������ͬ��
��2����������=ÿ����Ըƿ����������������
��3�����ݽ����ɱ��ɵ��Ա�����ȡֵ����϶��κ����Ĺ�ϵʽ���������Ӧ���������
�����������1��y��x��һ�κ�������y=kx+b��
ͼ����㣨10��300������12��240����
![]() ��
��
���![]() ��
��
��y=-30x+600��
��x=14ʱ��y=180����x=16ʱ��y=120��
���㣨14��180������16��120�����ں���y=-30x+600ͼ���ϣ�
��y��x֮��ĺ�����ϵʽΪy=-30x+600��
��2��w=��x-6����-30x+600��=-30x2+780x-3600��
��w��x֮��ĺ�����ϵʽΪw=-30x2+780x-3600��
��3��������ã�6��-30x+600����900��
���x��15��
w=-30x2+780x-3600ͼ��Գ���Ϊ��x=-![]() =-
=-![]() =13��
=13��
��a=-30��0��
�������߿������£���x��15ʱ��w��x�������С��
����x=15ʱ��w���=1350��
����15Ԫ/���ļ۸�����������Ըƿ�ɻ���������1350Ԫ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�