题目内容
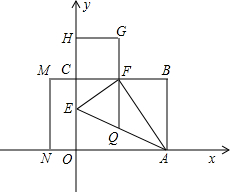
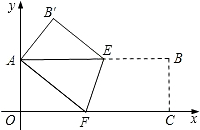
如图所示,将矩形OABC沿AE折叠,使点O恰好落在BC上F处,以CF为边作正方形CFGH,延长BC至M,使CM=|CE-EO|,再以CM、CO为边作矩形CMNO.(1)试比较EO、EC的大小,并说明理由;
(2)令m=
| S四边形CFGH |
| S四边形CMNO |
(3)在(2)的条件下,若CO=1,CE=
| 1 |
| 3 |
| 2 |
| 3 |
(4)在(3)的条件下,若抛物线y=mx2+bx+c与线段AB交于点P,试问在直线BC上是否存在点K,使得以P、B、K为顶点的三角形与△AEF相似?若存在,请求直线KP与y轴的交点T的坐标;若不存在,请说明
 理由.
理由.
分析:(1)根据折叠的条件得到EO=EF,在直角△CEF中,斜边大于直角边,因而EF>EC故EO>EC
(2)四边形CFGH与四边形CNMO的面积可以用直角△CEF的面积,可以证明四边形CFGH与四边形CNMO的面积相等.因而就可以求出m的值.
(3)已知OC=1,可以得到C点的坐标是(0,1),易证△EFQ是等边三角形,已知QF=
就可以求出Q点的坐标,把C,Q点的坐标代入函数y=mx2+bx+c,就可以求出b,c的值,就可以得到函数的解析式.
(4)过Q作y轴的垂线,已知E,Q点的坐标,可以根据三角形相似,求出OA的长,就可以求出P点的横坐标,进而求出P点的坐标.
若△PBK与△AEF相似,根据相似三角形的对应边的比相等,可以求出BK的值,即得到K的坐标.
(2)四边形CFGH与四边形CNMO的面积可以用直角△CEF的面积,可以证明四边形CFGH与四边形CNMO的面积相等.因而就可以求出m的值.
(3)已知OC=1,可以得到C点的坐标是(0,1),易证△EFQ是等边三角形,已知QF=
| 2 |
| 3 |
(4)过Q作y轴的垂线,已知E,Q点的坐标,可以根据三角形相似,求出OA的长,就可以求出P点的横坐标,进而求出P点的坐标.
若△PBK与△AEF相似,根据相似三角形的对应边的比相等,可以求出BK的值,即得到K的坐标.
解答:解:(1)EO>EC,理由如下:
由折叠知,EO=EF,在Rt△EFC中,EF为斜边,
∴EF>EC,
故EO>EC.
(2)m为定值,理由如下:
∵S四边形CFGH=CF2=EF2-EC2=EO2-EC2=(EO+EC)(EO-EC)=CO•(EO-EC),
S四边形CMNO=CM•CO=|CE-EO|•CO=(EO-EC)•CO,
∴m=
=1.
(3)∵CO=1,CE=
,QF=
,
∴EF=EO=1-
=
=QF,
∴cos∠FEC=
,
∴∠FEC=60°,
∴∠FEA=
=60°=∠OEA,∠EAO=30°,
∴△EFQ为等边三角形,EQ=
.
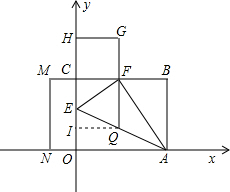
作QI⊥EO于I,EI=
EQ=
,IQ=
EQ=
,
∴IO=
-
=
,
∴Q点坐标为(
,
).
∵抛物线y=mx2+bx+c过点C(0,1),Q(
,
),m=1,
∴可求得b=-
,c=1,
∴抛物线解析式为y=x2-
x+1.
(4)由(3),AO=
EO=
,
当x=
时,y=(
)2-
×
+1=
<AB,
∴P点坐标为(
,
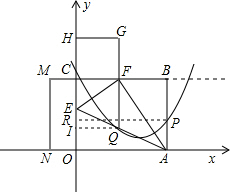
),
∴BP=1-
=
AO.
方法1:若△PBK与△AEF相似,而△AEF≌△AEO,则分情况如下:
①
=
时,BK=
,
∴K点坐标为(
,1)或(
,1);
②
=
时,BK=
,
∴K点坐标为(
,1)或(0,1).
故直线KP与y轴交点T的坐标为(0,-
)或(0,
)或(0,-
)或(0,1).
方法2:若△BPK与△AEF相似,由(3)得:∠BPK=30°或60°.
过P作PR⊥y轴于R,则∠RTP=60°或30°.
①当∠RTP=30°时,RT=
×
=2,
②当∠RTP=60°时,RT=
÷
=
,
∴T1(0,
),T2(0,-
),T3(0,-
),T4(0,1).
由折叠知,EO=EF,在Rt△EFC中,EF为斜边,
∴EF>EC,
故EO>EC.
(2)m为定值,理由如下:
∵S四边形CFGH=CF2=EF2-EC2=EO2-EC2=(EO+EC)(EO-EC)=CO•(EO-EC),
S四边形CMNO=CM•CO=|CE-EO|•CO=(EO-EC)•CO,
∴m=
| S四边形CFGH |
| S四边形CMNO |
(3)∵CO=1,CE=
| 1 |
| 3 |
| 2 |
| 3 |
∴EF=EO=1-
| 1 |
| 3 |
| 2 |
| 3 |
∴cos∠FEC=
| 1 |
| 2 |
∴∠FEC=60°,
∴∠FEA=
| 180°-60° |
| 2 |
∴△EFQ为等边三角形,EQ=
| 2 |
| 3 |
作QI⊥EO于I,EI=
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 3 |

∴IO=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴Q点坐标为(
| ||
| 3 |
| 1 |
| 3 |
∵抛物线y=mx2+bx+c过点C(0,1),Q(
| ||
| 3 |
| 1 |
| 3 |
∴可求得b=-
| 3 |
∴抛物线解析式为y=x2-
| 3 |
(4)由(3),AO=
| 3 |
| 2 |
| 3 |
| 3 |
当x=
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 1 |
| 3 |
∴P点坐标为(
2
| ||
| 3 |
| 1 |
| 3 |

∴BP=1-
| 1 |
| 3 |
| 2 |
| 3 |
方法1:若△PBK与△AEF相似,而△AEF≌△AEO,则分情况如下:
①
| BK | ||
|
| ||||
|
2
| ||
| 9 |
∴K点坐标为(
4
| ||
| 9 |
8
| ||
| 9 |
②
| BK | ||||
|
| ||
|
2
| ||
| 3 |
∴K点坐标为(
4
| ||
| 3 |
故直线KP与y轴交点T的坐标为(0,-
| 5 |
| 3 |
| 7 |
| 3 |
| 1 |
| 3 |
方法2:若△BPK与△AEF相似,由(3)得:∠BPK=30°或60°.
过P作PR⊥y轴于R,则∠RTP=60°或30°.
①当∠RTP=30°时,RT=
2
| ||
| 3 |
| 3 |
②当∠RTP=60°时,RT=
2
| ||
| 3 |
| 3 |
| 2 |
| 3 |
∴T1(0,
| 7 |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
点评:本题主要考查了待定系数法求函数解析式,以及相似三角形的性质,相似三角形的对应边的比相等.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
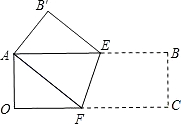


 已知,如图所示,矩形OABC在平面直角坐标系中,矩形各顶点分别为O(0,0),A(0,6),B(8,6),C(8,0).点D(0,3)在OA上,点E(4,0)在OC上,连接DE,将△DOE绕O点逆时针旋转,旋转角为α(0°<α<360°),得到△D′OE′,连接AD′,当∠AD′O=90°时,
已知,如图所示,矩形OABC在平面直角坐标系中,矩形各顶点分别为O(0,0),A(0,6),B(8,6),C(8,0).点D(0,3)在OA上,点E(4,0)在OC上,连接DE,将△DOE绕O点逆时针旋转,旋转角为α(0°<α<360°),得到△D′OE′,连接AD′,当∠AD′O=90°时, 在直角坐标系中,OA=6,OC=8,若将矩形折叠,使点B与O重合,得到折痕EF。
在直角坐标系中,OA=6,OC=8,若将矩形折叠,使点B与O重合,得到折痕EF。 
