题目内容
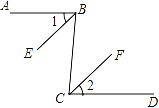
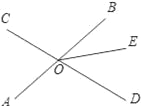
【题目】如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.
(1)求∠BOE和∠AOE的度数;
(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.

【答案】(1)∠AOE的度数是156°;
(2)∠DOF的度数是138°或42°.
【解析】(1)设∠BOE=x,根据题意列出方程,解方程即可;
(2)分射线OF在∠AOD的内部和射线OF在∠BOC的内部两种情况,根据垂直的定义计算即可.
解:(1)∵∠AOC=72°,
∴∠BOD=72°,∠AOD=108°,
设∠BOE=x,则∠DOE=2x,
由题意得,x+2x=72°,
解得,x=24°,
∴∠BOE=24°,∠DOE=48°,
∴∠AOE=156°;
(2)若射线OF在∠BOC的内部,
∠DOF=90°+48°=138°,
若射线OF在∠AOD的内部,
∠DOF=90°﹣48°=42°,
∴∠DOF的度数是138°或42°.
“点睛”本题考查的是对顶角和邻补角的概念和性质以及垂直的定义,掌握对顶角相等、邻补角的和是180°是解题的关键,要灵活运用分类讨论思想解题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 |
则这些运动员成绩的中位数、众数分别为( )
A. 1.70,1.75 B. 1.70,1.70
C. 1.65,1.75 D. 1.65,1.70