��Ŀ����
����Ŀ��2008��5��12��14ʱ28���Ĵ��봨��������8.0��ǿ������ij�нӵ��ϼ�֪ͨ�������ɳ��ס��������������С��˳���ͬһ·�߸ϸ��������480ǧ����������������ҪЯ��һЩ�������ʣ��ȼ���ٳ���1.25Сʱ���Ӽ������ʱ��ʼ��ʱ����ͼ�е����ߡ��߶ηֱ��ʾ�ס������������·��y����ǧ�ף���y����ǧ�ף���ʱ��x��Сʱ��֮��ĺ�����ϵ��Ӧ��ͼ�������ͼ�����ṩ����Ϣ������������⣺
��1�����������������ϣ�������;��ͣ���� Сʱ��
��2������������ų����Ϻ��������ٸ������������ʼ�����������ų�����ʱ����������·���Ƕ���ǧ�ף�
��3��Ϊ�˱�֤��ʱ���磬�ס��������ڵ�һ������ʱԼ���˺�����֮���·�̲�����25ǧ�ף���ͨ������˵������ͼ������ʾ���߷��Ƿ����Լ����
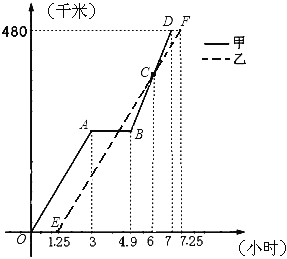
���𰸡�(1)��1.9��(2)��270ǧ�ף�(3)������Լ��.
��������
���������(1)�������߶�AB��x��ƽ�У�����3ʱ��4.9ʱ���ʱ���ڼ���ͣ����;�У�����ͣ����ʱ��Ϊ1.9ʱ��(2)���۲�ͼ���֪��B����������Ǽ�����������ų�����ʱ��������·�̵�ǧ������������õ�B�������ǽ��(2)��Ĺؼ��������Ҫ���ֱ��EF��ֱ��BD�Ľ���ʽ����EF���㣨1.25��0������7.25��480������������������꼴�������ֱ�ߵĽ���ʽ��Ȼ����x=6�����������C�������꣬�����D��7��480���������Ϳ����CD��BD�Ľ���ʽ���Ӷ����B������ꣻ(3)����ͼ���֪���ס��������һ����������B��D�����Զ���ڵ�B��ʱ��x=4.9�������ʱ��y����y�����ڵ�D��x=7��Ҳ�����ʱ��y����y�����ֱ�ͬ25�Ƚϼ��ɣ�
���������(1)��1.9��
(2)����ֱ��EF�Ľ���ʽΪy��=kx+b�� ����E��1.25��0������F��7.25��480������ֱ��EF�ϣ�
��![]() �� ���
�� ���![]() ��ֱ��EF�Ľ���ʽ��y��=80x��100��
��ֱ��EF�Ľ���ʽ��y��=80x��100��
����C��ֱ��EF�ϣ��ҵ�C�ĺ�����Ϊ6�� ����C��������Ϊ80��6��100=380��
����C�������ǣ�6��380���� ��ֱ��BD�Ľ���ʽΪy��=mx+n��
����C��6��380������D��7��480����ֱ��BD�ϣ� ��![]() �� ���
�� ���![]() ��
��
��BD�Ľ���ʽ��y��=100x��220�� ��B����ֱ��BD���ҵ�B�ĺ�����Ϊ4.9������y����B��4.9��270����
���������ų�����ʱ����������·����270ǧ�ף�
(3)������Լ���� ��ͼ���֪���ס��������һ����������B��D�����Զ��
�ڵ�B����y����y��=80��4.9��100����100��4.9��220��=22ǧ�ף�25ǧ�ף�
�ڵ�D��y����y��=100��7��220����80��7��100��=20ǧ�ף�25ǧ�ף� ����ͼ������ʾ���߷�����Լ����