Question

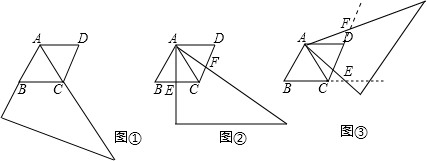
用两个全等的等边△ABC和△ACD拼成菱形ABCD，把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB、AC重合．将三角尺绕着点A逆时针方向旋转．

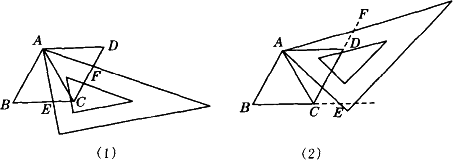
(1)当三角尺的两边分别与菱形的两边BC、CD相交于点E、F(如图(1))，通过观察或测量BE和CF的长度，你能得出什么结论？并证明你的结论．

(2)当三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F(如图(2))，你在(1)中得到的结论还成立吗？简要说明理由．

Answer 1

答案：
解析：

解答：(1)经测量知BE＝CF．理由如下： 　　∵∠BAE＋∠EAC＝∠BAC＝60°，∠CAF＋∠EAC＝∠EAF＝60° 　　∴∠BAE＝∠CAF 　　∵△ABC和AACD是两个全等的等边三角形 　　∴AB＝AC，∠B＝∠ACF 　　∴△ABE≌△ACF 　　∴BE＝CF 　　(2)经测量知仍然有BE＝CE．理由如下： 　　∵∠BAE－∠EAC＝∠BAC＝60°，∠CAF－∠EAC＝∠EAF＝60° 　　∴∠BAE＝∠CAF 　　∵△ABC和△ACD是两个全等的等边三角形 　　∴AB＝AC，∠B＝∠ACF 　　∴△ABE≌△ACF 　　∴BE＝CF 　　思路与技巧：第(1)小题要找到BE和CF的关系，可以直观地看出△ABE和△ACF全等，如果能证明出这个结论，那么BE和CF的关系是相等．由菱形的条件，可以得到边相等的关系，由等边三角形及三角尺的60°角可以得到角相等的关系，因此三角形的全等不难得证．第(2)小题同样可以直观地看出△ABE和△ACF全等，所以我们利用已知条件证明出这个结论即可． 　　评析：本题要求先通过操作实践获得结论，然后再给予证明，体现了《数学课程标准》提出的相关要求，此外本题探索的是运动着的图形的性质，所以这种试题是中考的热点题型．