题目内容
已知一条抛物线经过A(0,3),B(4,6)两点,对称轴是x=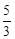 .
.
(1)求这条抛物线的关系式.
(2)证明:这条抛物线与x轴的两个交点中,必存在点C,使得对x轴上任意点D都有AC+BC≤AD+BD.
【答案】
(1) y=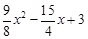 (2)证明见解析
(2)证明见解析
【解析】本题主要考查了抛物线与x轴的交点和待定系数法求二次函数解析式
(1)先设出函数的解析式:y=ax2+bx+c,根据抛物线经过A(0,3),B(4,6)两点,用待定系数法求出函数的解析式;
(2)令y=0,得到方程,根据方程根与系数的关系求出抛物线与x轴的两个交点,再根据三角形任意两边之和大于第三边,来证明.
(1)解:设所求抛物线的关系式为y=ax2+bx+c,
∵A(0,3),B(4,6),对称轴是直线x=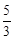 .
.
∴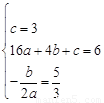 , 解得
, 解得
∴y=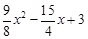 .
.
(2)证明:令y=0,得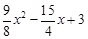 =0, ∴
=0, ∴ 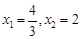
∵A(0,3),取A点关于x轴的对称点E,∴E (0,-3).
设直线BE的关系式为y=kx-3,把B(4,6)代入上式,得6=4k-3,
∴k=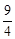 ,∴y=
,∴y=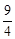 x-3
.
x-3
.
由 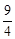 x-3=0,得x=
x-3=0,得x=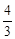 .
.
故C为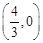 ,C点与抛物线在x轴上的一个交点重合,
,C点与抛物线在x轴上的一个交点重合,
在x轴上任取一点D,在△BED中,BE< BD+DE.
又∵BE=EC+BC,EC=AC,ED=AD,∴AC+BC<AD+BD.
若D与C重合,则AC+BC=AD+BD. ∴AC+BC≤AD+BD.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 .
. .
.