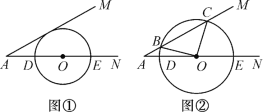Question

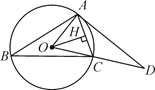
【题目】如图，△ABC内接于⊙O，OH⊥AC于点H，过A点的切线与OC的延长线交于点D，∠B＝30°，OH＝5，请求出：

(1)∠AOC的度数；

(2)劣弧的长；(结果保留π)

(3)线段AD的长．(结果保留根号)

Answer 1

【答案】（1）60°；（2）；（3）10.

【解析】

（1）由圆周角定理得，∠AOC=2∠B=60°；

（2）由等腰三角形的性质：底边上的高与顶角的平分线重合知，∠AOH=30°，故可由余弦

的概念求得AO的值，进而由弧长公式求得弧AC的长；

（3）在Rt△AOD中，可由正切的概念求得AD的长．

（1）∠AOC=2∠B=60°；

（2）在△AOC中，

∵OH⊥AC，OA=OC，

∴OH是等腰三角形AOC的底边AC上的高，

∴∠AOH=∠AOC=30°，

∴AO=，

∴的长=，

∴的长是；

（3）∵AD是切线，

∴AD⊥OA，

∵∠AOC=60°，

∵tan60°=，

∴AD=AOtan60°=10，

∴线段AD的长是10．