题目内容
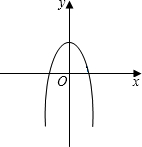
函数y=ax2（a≠0）与直线y=2x-3交于点（1，b）。
（1）求a和b的值；
（2）求抛物线y=ax2的解析式，并求顶点坐标及对称轴；
（3）x取何值时，二次函数y=ax2中的y随x的增大而增大？
（4）求抛物线和直线y=-2的两个交点与抛物线顶点所构成的三角形的面积。
（1）求a和b的值；
（2）求抛物线y=ax2的解析式，并求顶点坐标及对称轴；
（3）x取何值时，二次函数y=ax2中的y随x的增大而增大？
（4）求抛物线和直线y=-2的两个交点与抛物线顶点所构成的三角形的面积。
| 解：（1）把x=1，y=b代入y=2x-3，解得b=-1， ∴交点坐标是（1，-1）， 再把x=1，y=-1代入y=ax2， 解得a=-1， ∴a=-1，b=-1； （2）抛物线的解析式为y=-x2，顶点坐标为（0，0），对称轴为y轴； （3）当x＜0时，y随x的增大而增大； （4）设直线y=-2与抛物线y=-x2交于A、B两点，如图， 则  ，∴  。 |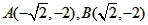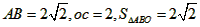
 |
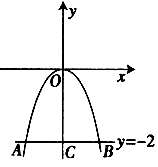练习册系列答案
相关题目
15、函数y=ax2+bx+c的图象如图所示，且线段OM与ON相等，则a，b，c之间的关系为
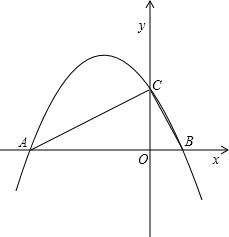如图所示，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于C（0，2），若∠ACB=90°，
如图，二次函数y=ax2+bx+c的图象与x轴交于B、C两点，与y轴交于点A（0，-3），∠ABC=45°，∠ACB=60°，求这个二次函数解析式．
已知正比例函数y=ax与反比例函数
